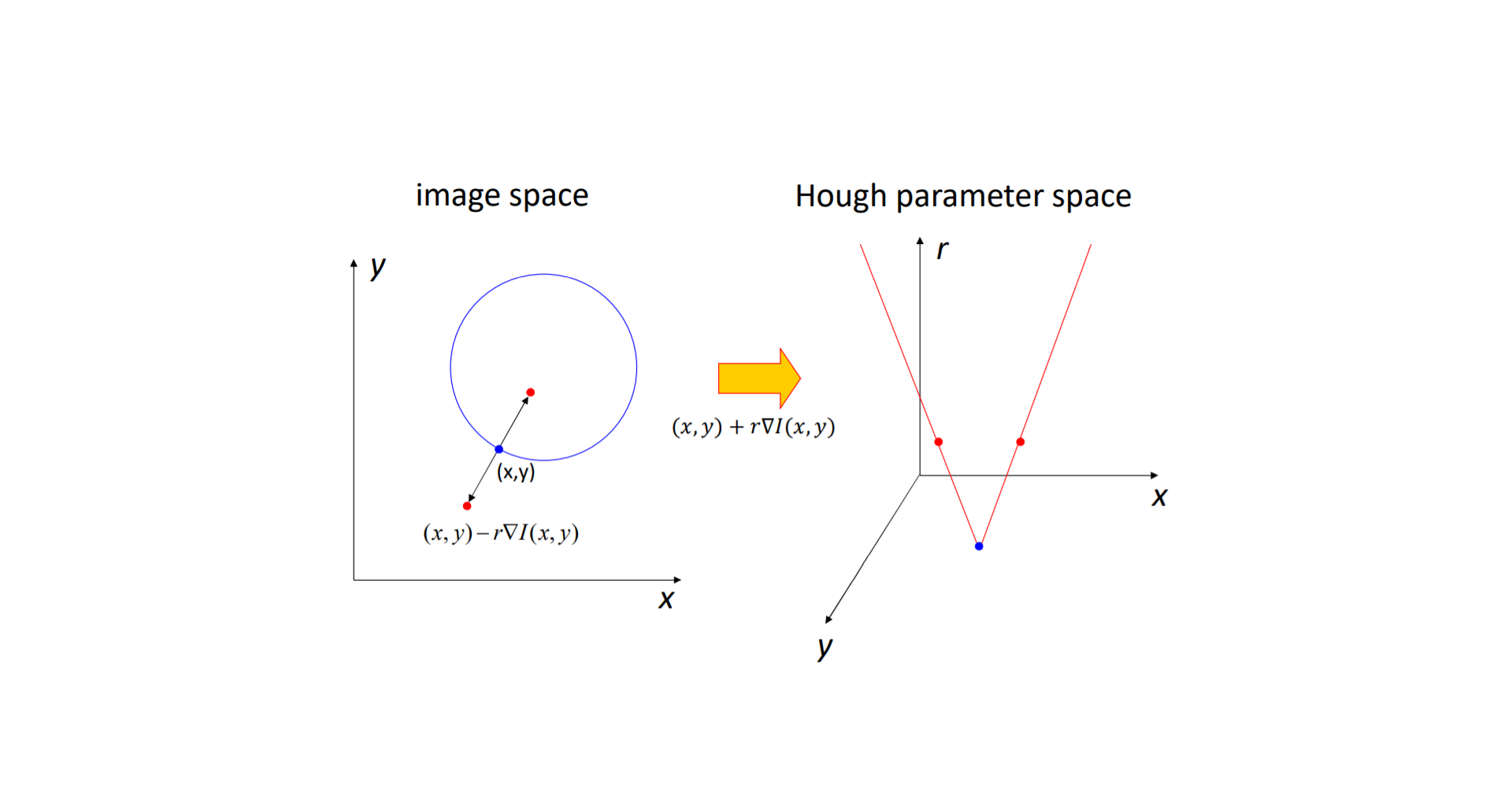
图像分割(Segmentation)——K-Means, 最小割, 归一化图割
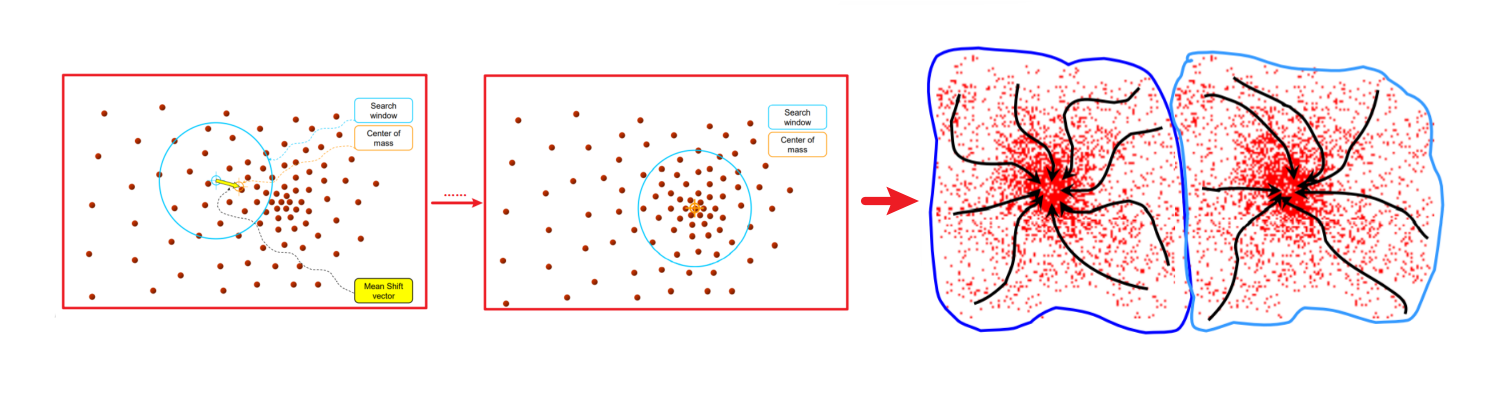
图像分割是将图片将相似的部分分割成相同的块
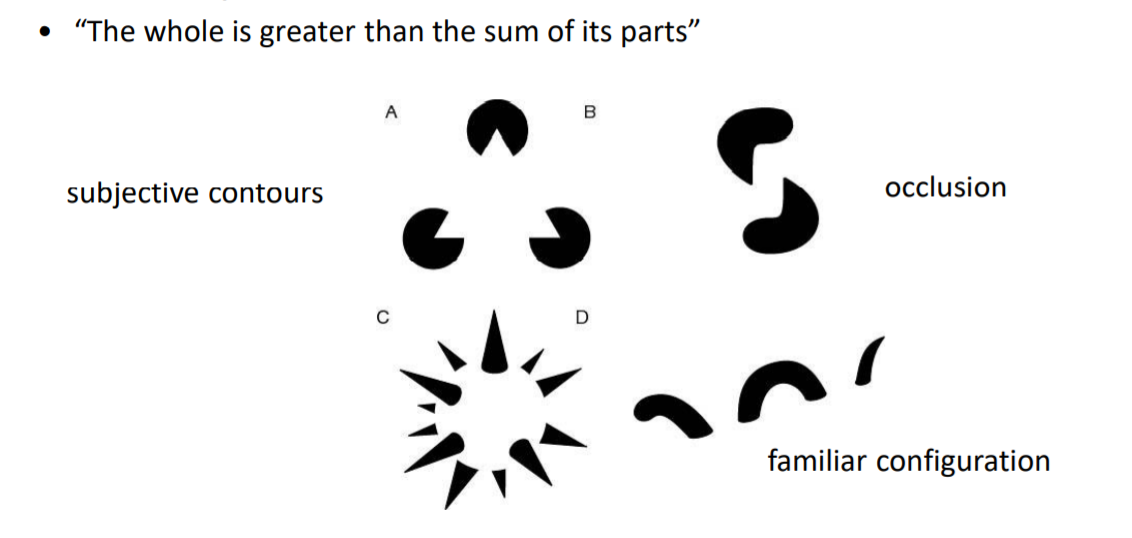
1 Gestalt理论
解释物体分割的底层原理 将同一个东西群组在一起,集合中的元素可以具有由关系产生的属性
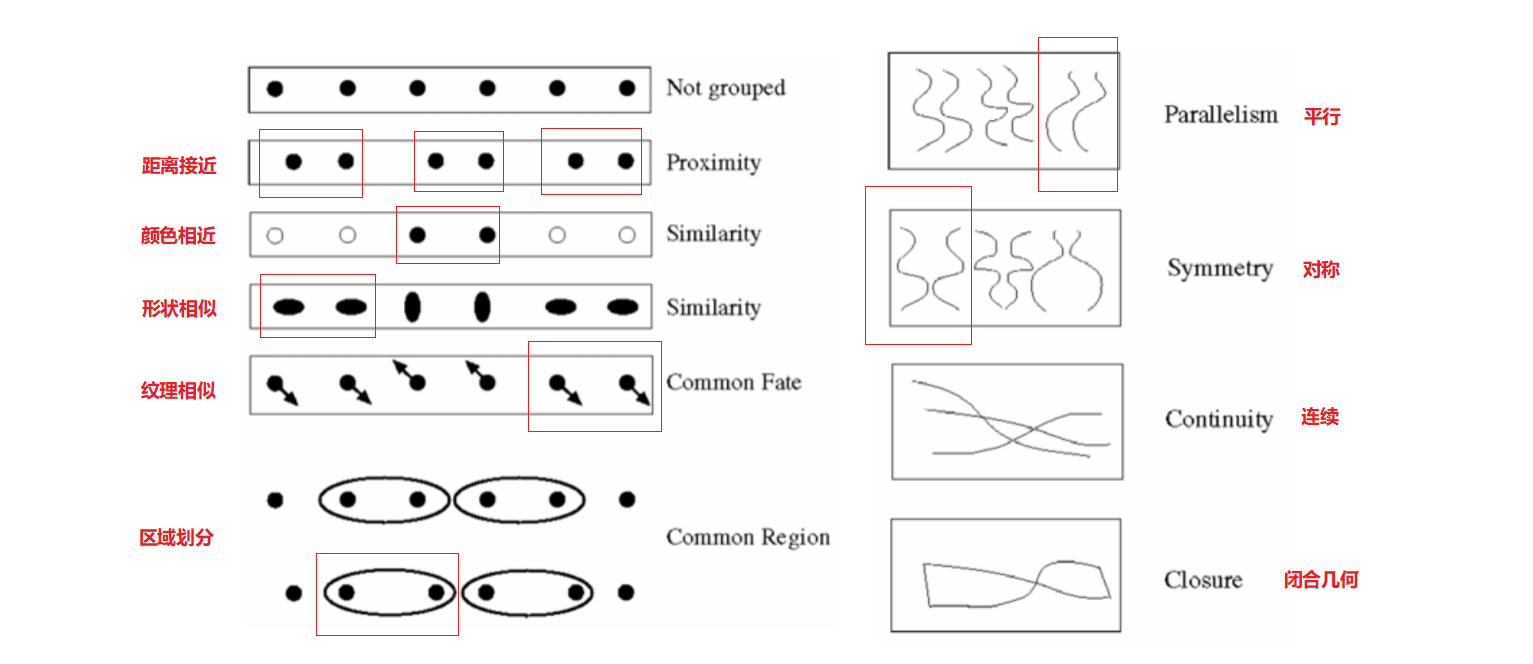
Gestalt中常见的一些分组的情况
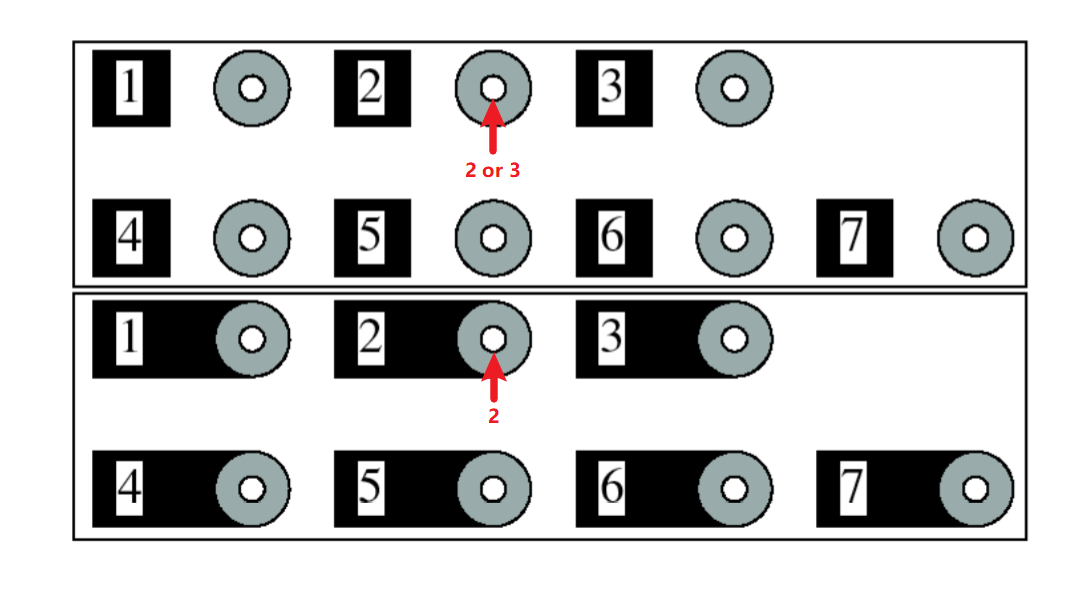
现实生活中的分组现象
2 K-Means聚类
主要思想:相似的像素应该属于同一类
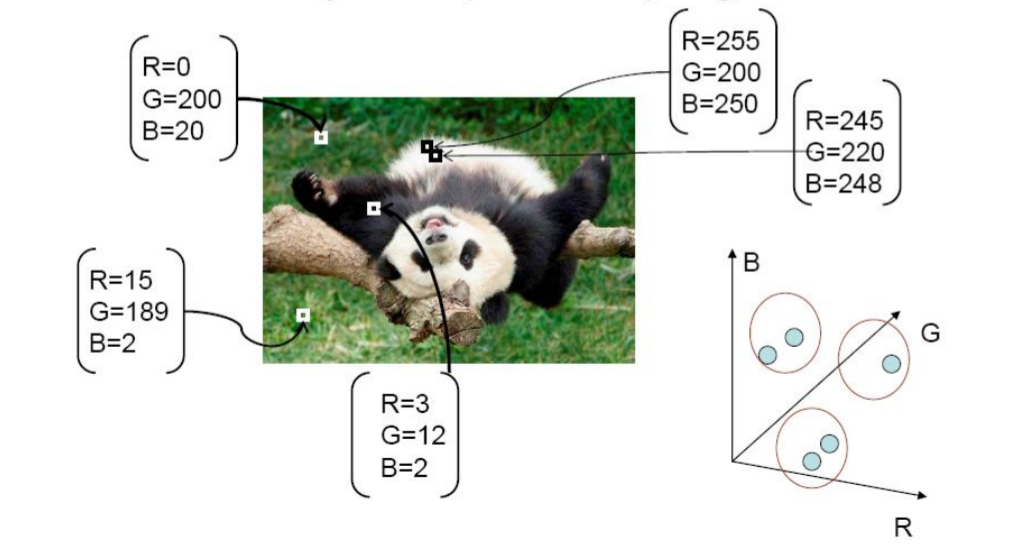
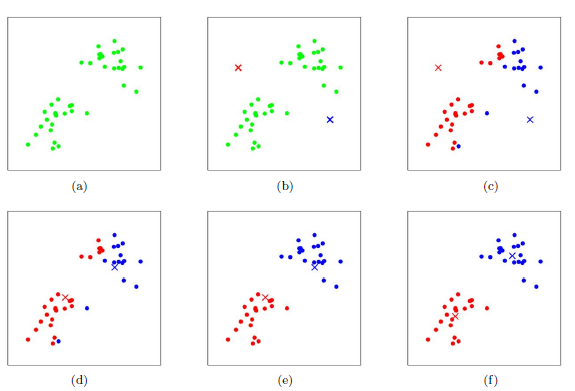
K-Means算法: “物以类聚、人以群分”:
首先输入k的值,即我们希望将数据集经过聚类得到k个分组。
从数据集中随机选择k个数据点作为初始大哥(质心,Centroid)
对集合中每一个小弟,计算与每一个大哥的距离(距离的含义后面会讲),离哪个大哥距离近,就跟定哪个大哥。
这时每一个大哥手下都聚集了一票小弟,这时候召开人民代表大会,每一群选出新的大哥(其实是通>过算法选出新的质心)。
如果新大哥和老大哥之间的距离小于某一个设置的阈值(表示重新计算的质心的位置变化不大,趋于>稳定,或者说收敛),可以认为我们进行的聚类已经达到期望的结果,算法终止。
如果新大哥和老大哥距离变化很大,需要迭代3~5步骤。
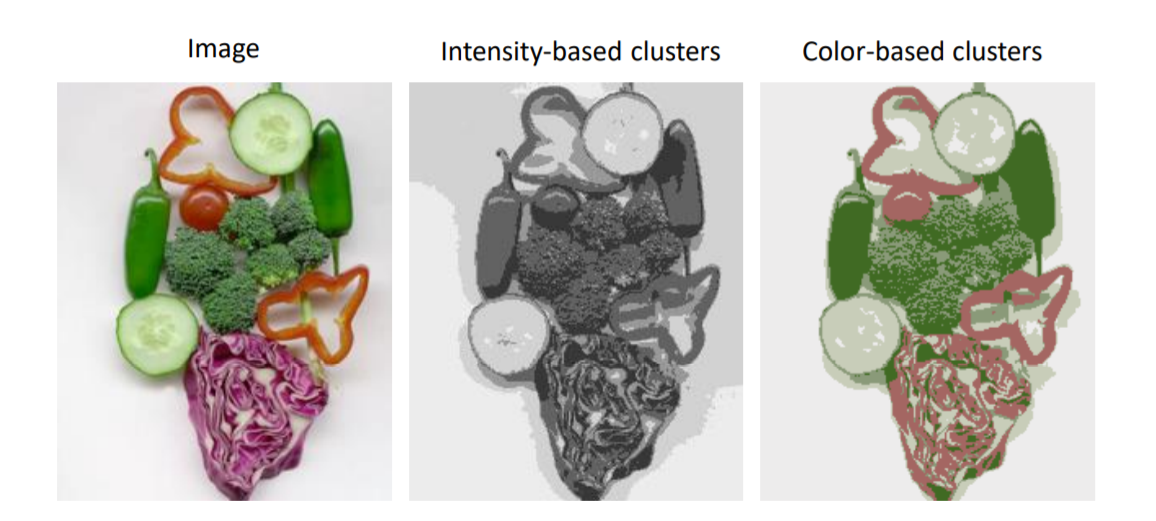
基于灰度值或颜色的K-means聚类本质上是对图像属性的矢量量化
- 语义分割:将不同位置上同样的物品分成同一类(如上图三)使用(R, G, B)的三维向量描述像素
- 实列分割:将不同位置上同样的物品分成不同类,此时就需要考虑像素位置对分割的影响,使用(R, G, B, x, y)的五维向量描述像素
3 Mean shift 聚类
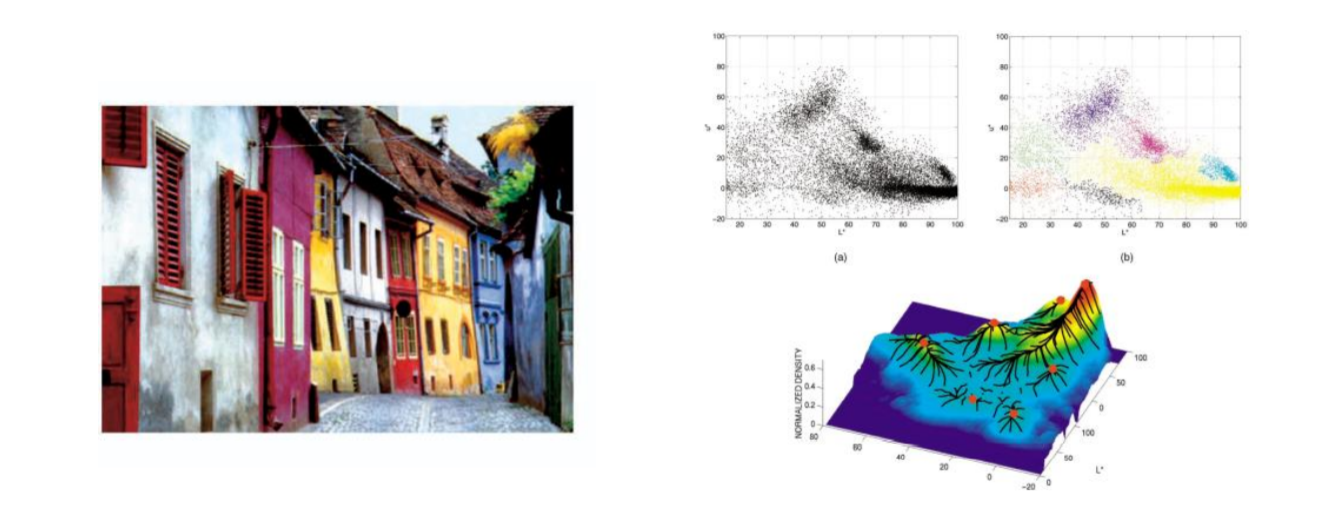
K-Means算法可以很简单的进行分割,但是初始值对结果的影响非常大,Mean Shift 算法处理时将像素密度的峰值作为初始值,在特征空间中寻找密度的模态或局部最大值
- 定义特征值:(color, gradients, texture, etc)
- 在单个特征点上初始化窗口
- 对每个窗口执行Mean Shift直到收敛
- 合并接近相同“峰值”或模式的窗口
分割实例:
- 算法计算量不大,在目标区域已知的情况下完全可以做到实时跟踪;
- 采用核函数直方图模型,对边缘遮挡、目标旋转、变形和背景运动不敏感。
缺点:
- 缺乏必要的模板更新;
- 跟踪过程中由于窗口宽度大小保持不变,当目标尺度有所变化时,跟踪就会失败;
- 当目标速度较快时,跟踪效果不好;
- 直方图特征在目标颜色特征描述方面略显匮乏,缺少空间信息。
4 Image as Graphs
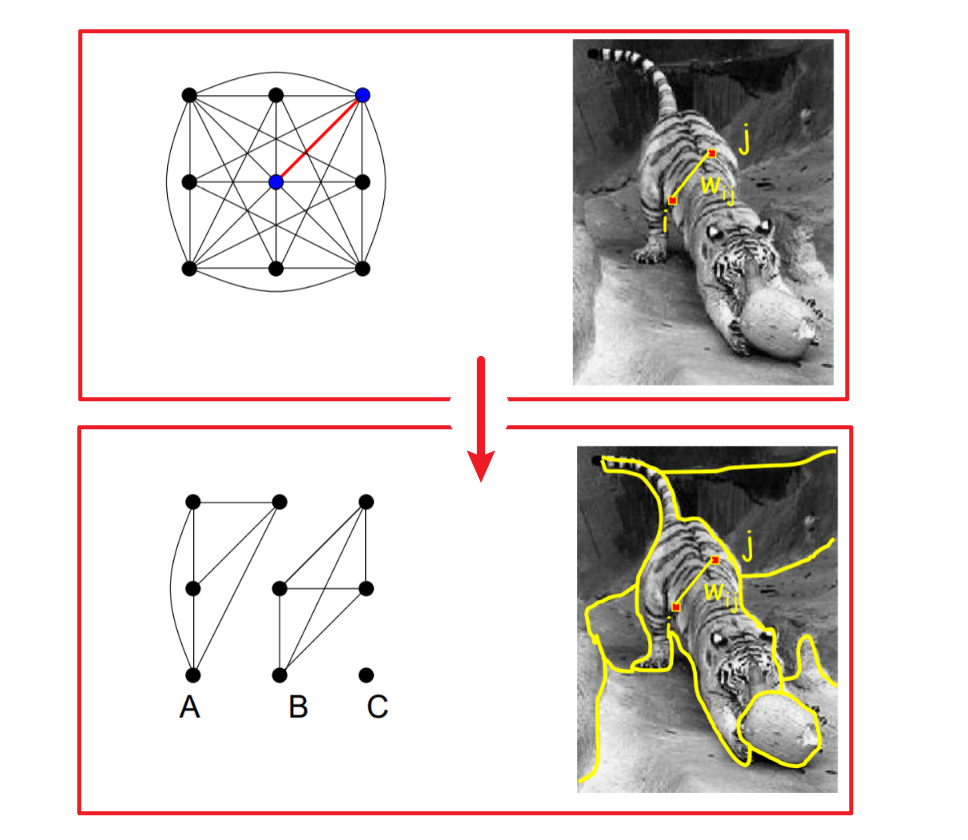
- 节点代表像素
- 每对节点之间代表边缘(或每对“足够接近”的像素)
- 每条边都根据两个节点的亲和力或相似性进行加权
- 找一条边将,将像素之间的联系切断
- 将切断的边的权重相加,使和最小(相似的像素应该在相同的部分,不同的像素应该在不同的部分)
定义权值 $$ exp(-\frac{1}{2\sigma^2}dist(X_i,X_j)^2) $$
-
假设用特征向量x表示每个像素,并定义一个适合于该特征表示的距离函数: $dist(X_i,X_j)^2$
-
然后利用广义高斯核将两个特征向量之间的距离转化为相似性
-
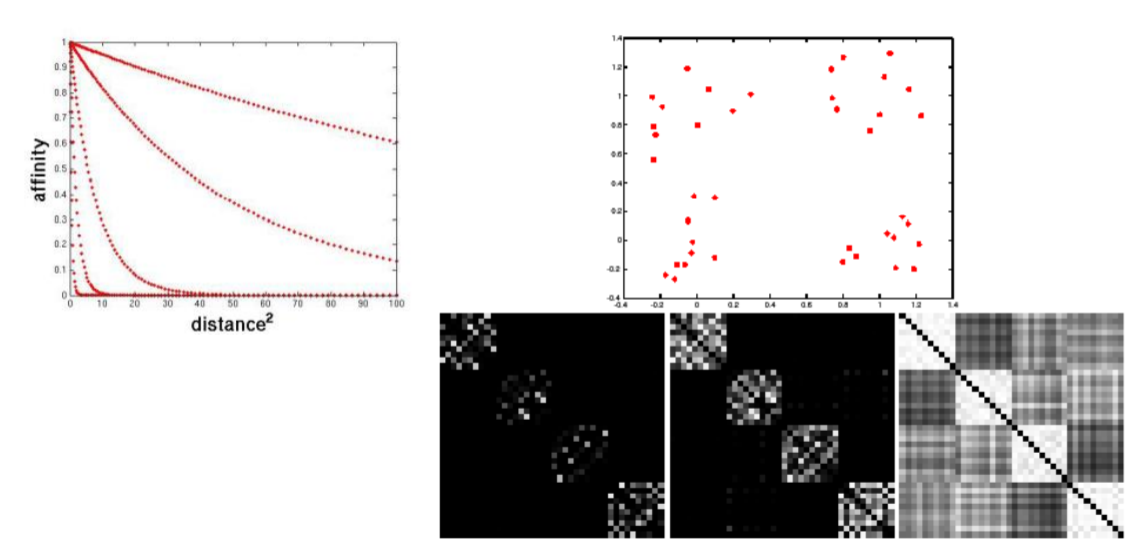
小的$\sigma$:仅群聚邻近点;大的$\sigma$:群聚距离远的点
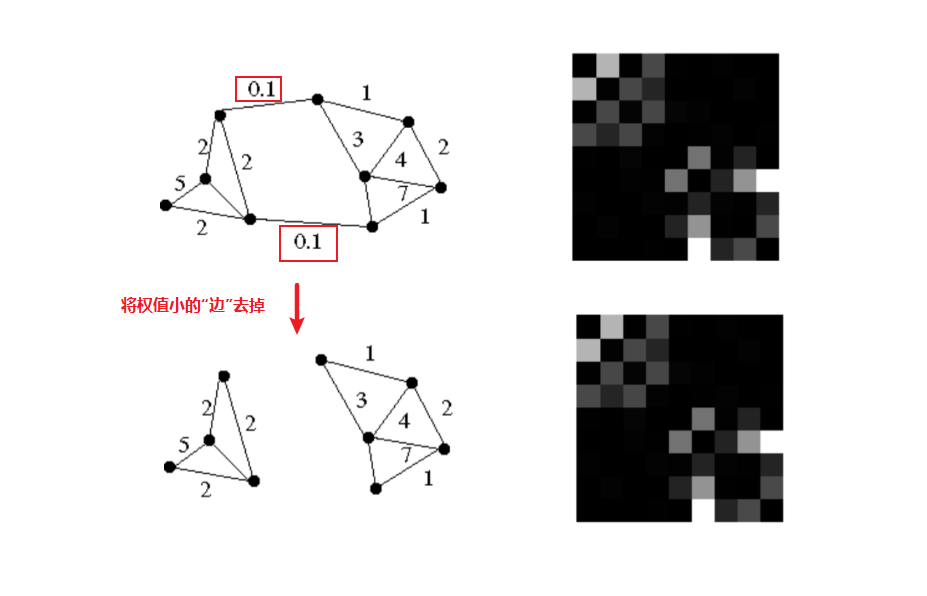
最小割:将权值小的边去掉
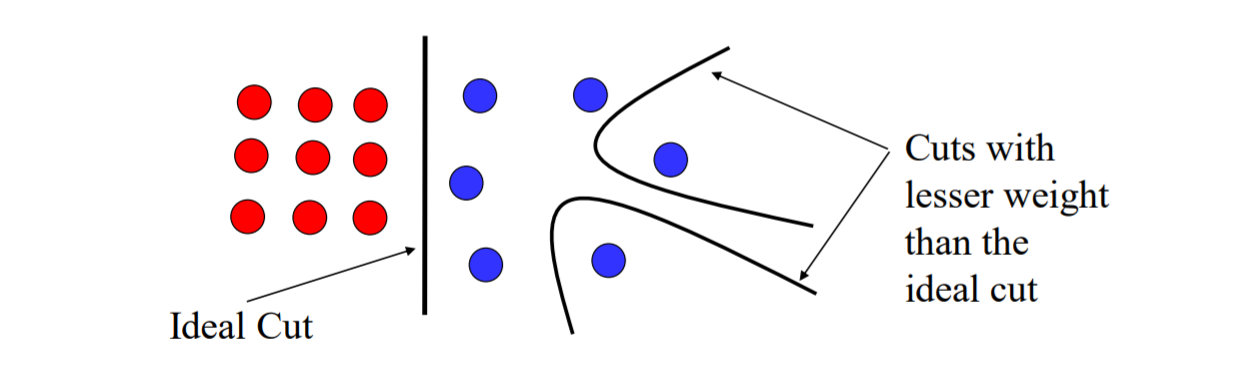
最小割中趋向于将点单独的割出来,就会导致分割出很多“小块”
归一化图割
$$ \frac{W(A,B)}{W(A,V)}+\frac{W(A,B)}{W(B,V)} $$
- $W(A,B)$:表示集合$A, B$中所有边的权重的和
- $W(A,V),W(B,V)$:分别表示分割后集合$A, B$内边的个数,当总的边数一定,其中一个$W$很大时,另一个就会很小,导致整个算式所计算的权重就会很大
-
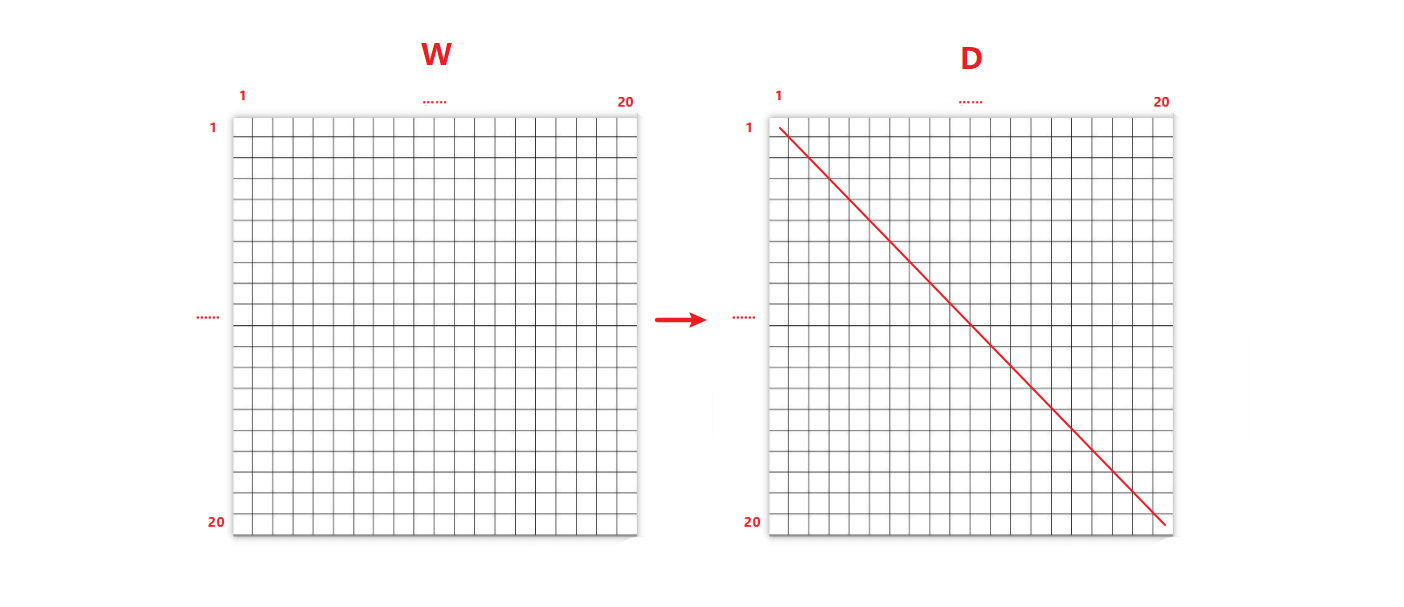
定义一个邻接关系矩阵$W$,$(i,j)$表示第i个像素与第j个像素之间的权重,是一个对称的矩阵
-
定义矩阵$D$,是一个对角的矩阵$D_{ii} = \Sigma_jW(i, j)$
$$ \frac{y^T(D-W)y}{y^TDy} $$
-
归一化图割权重计算:其中,y是指示向量,如果第i个特征点属于A,那么它在第i个位置的值应该为1,反之则为0;利用拉格朗日算法求权重第二小(最小的是0)的特征值对应的特征向量y:$(D-W)y=\lambda y$ 所求出的y不是[0,…,1,0,0…]而是存在小数的向量,需要设置一个门限,将大于门限的设置为1,小于门限的设置为0
-
使用特征向量y的项对图进行二分割
-
改变门限,迭代将图像分成多个区块,也可以使用K-Means将得到的特征向量分类,达到分割多块的效果
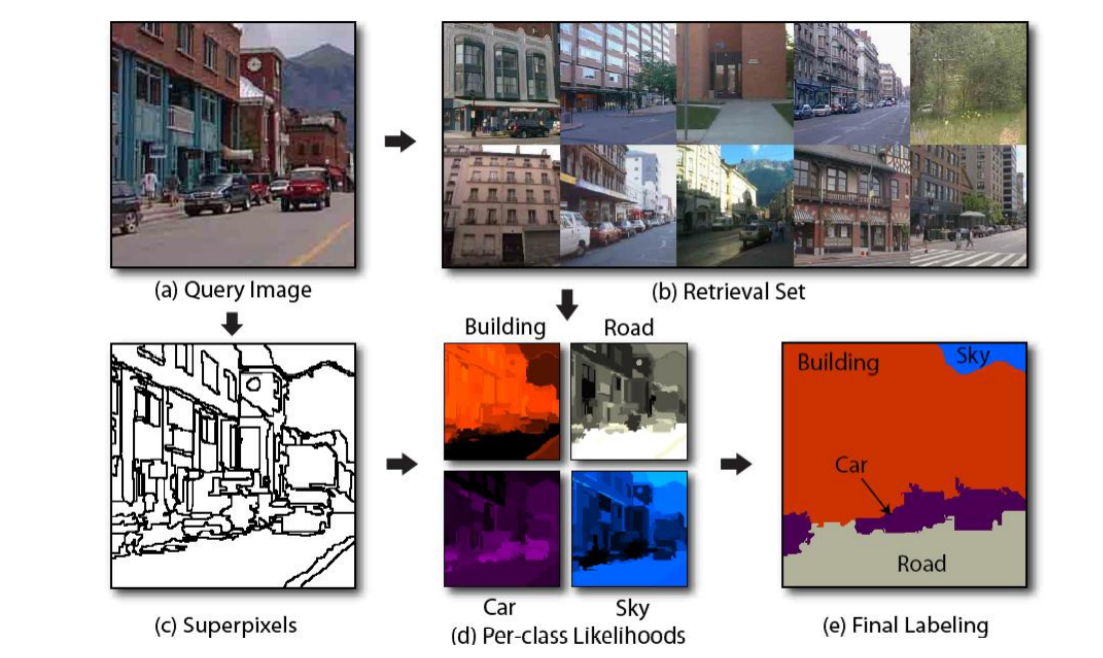
分割效果:
学习资源:北京邮电大学计算机视觉——鲁鹏