WYXOGO拟合(Fitting)
提取完边缘后如何使用数学模型来描述边缘？ 例如：在桌子上有几枚硬币，在经过边缘提取后，需要描述出硬币的圆心坐标和圆的大小
1 难点
- 噪声：噪声的存在使拟合的模型偏离真实的线
- 外点：在目标图形以外的线，如上图中的目标图形为“车”，左边的“栅栏”就是外点
- 目标图形部分被遮挡，使部分图形消失
2 最小二乘（Least Square）
针对点都在线上的一些简单模型
- 最小二乘
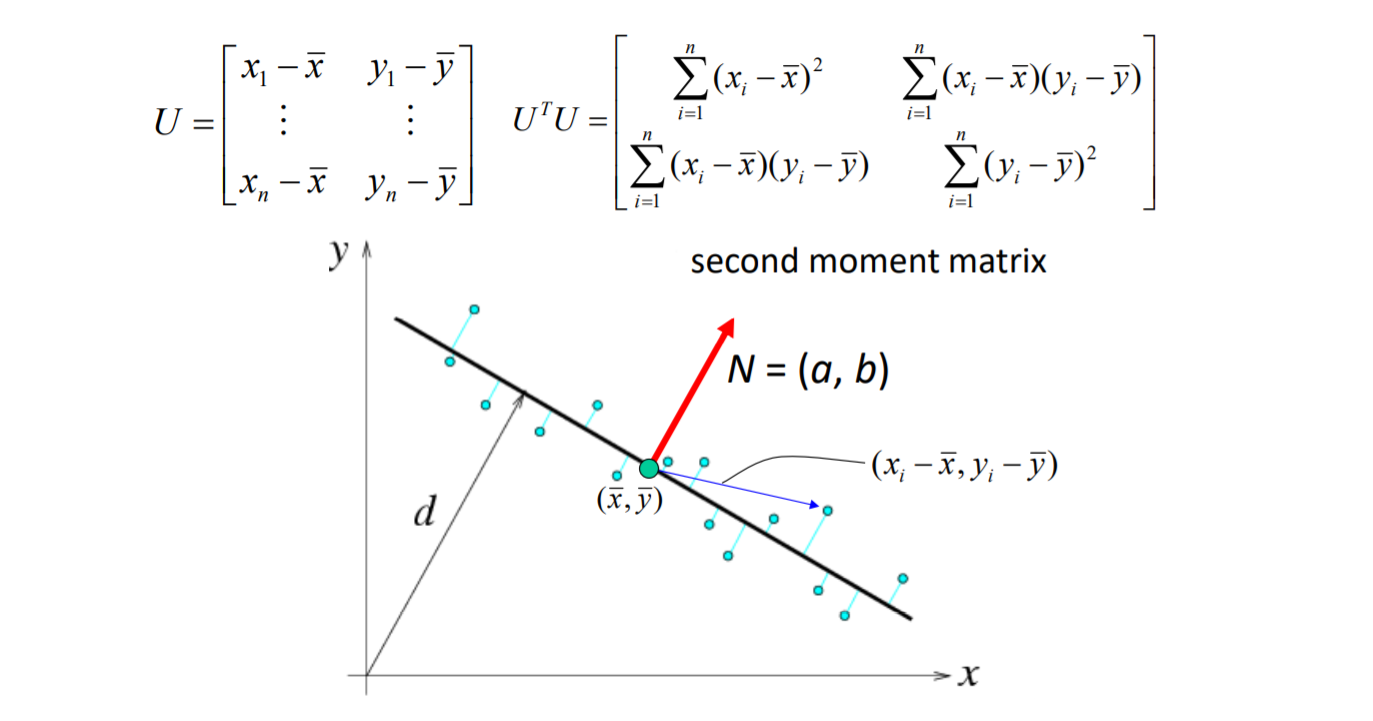
能量函数$E$描述的是所有的点与拟合的线在$y$方向上的差值的和，最后的目标是求出差值最小时的$(m,b)$即矩阵$B$作为这个模型的解
-
权最小二乘 当拟合的直线是平行$y$轴时就无法按照上面的公式计算$E$（最小二乘对旋转没有效果）
权最小二乘将点在$y$方向的距离改为对直线距离的平方，就可以避免旋转产生的问题 ，它的几何描述就是所有的向量$(x_i-\bar x,y_i-\bar y)$在向量$(a,b)$的投影的值最小
-
极大似然估计
使用概率分布的思想来理解权最小二乘，概率越大拟合效果越好，极大似然估计，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值，它提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。
如果通过极大似然估计，得到模型中参数$\mu$和$\sigma$的值，那么这个模型的均值和方差以及其它所有的信息我们就知道了。
3 Roubst Fitting & RANSAC
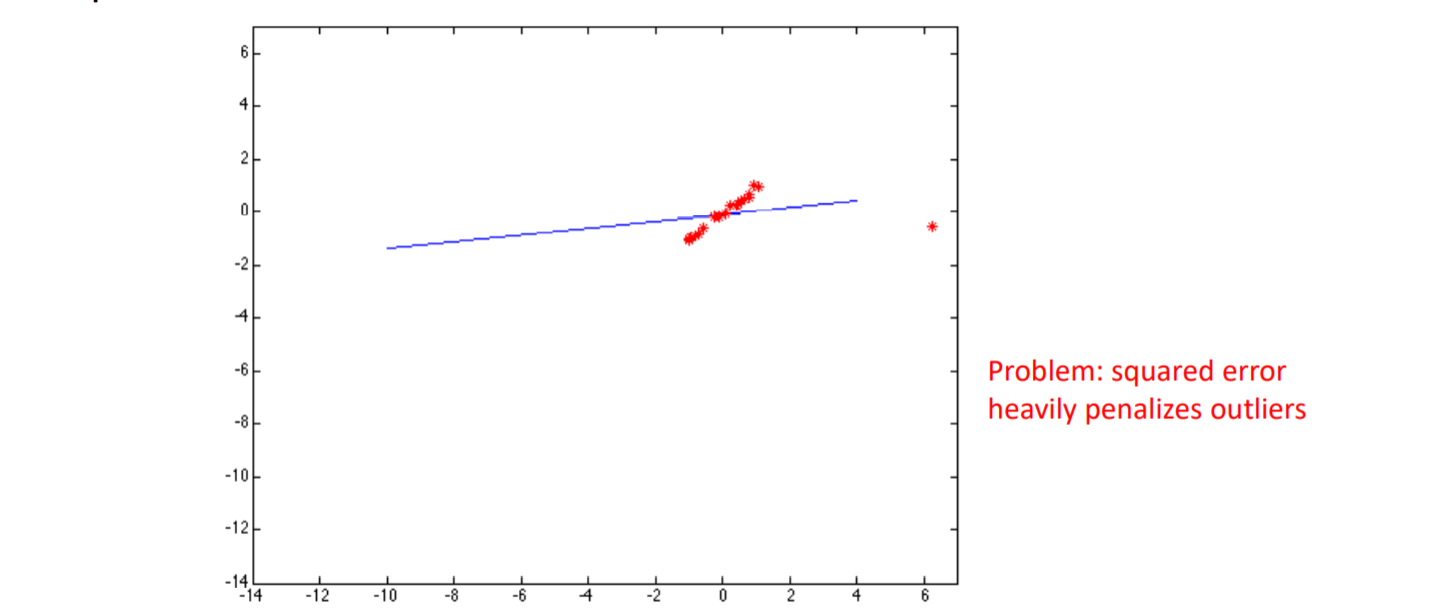
当存在外点时，普通的（权）最小二乘就无法很好的拟合模型
3.1 Roubst fitting（鲁棒拟合）
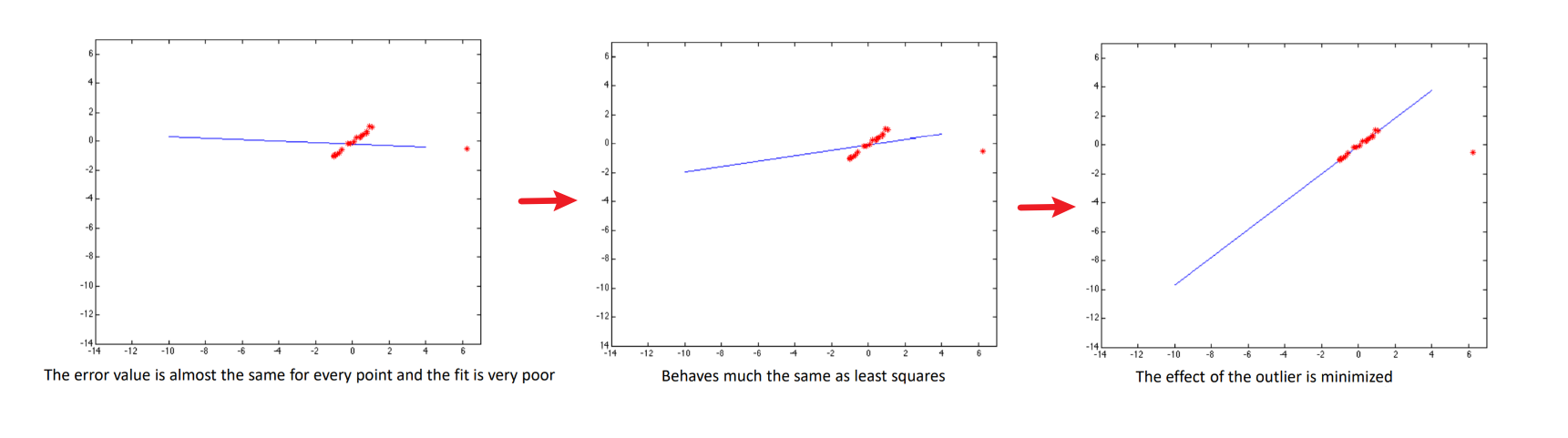
通过函数$\rho(u;\sigma)$将点到直线的距离$u$在较大的范围时对直线影响的贡献值缩小，$\sigma$为设置的参数，当参数越小对所取的预拟合模型的区域越小，例如当$\sigma=0.1$时，对超过2以后的区域几乎就不做考虑了
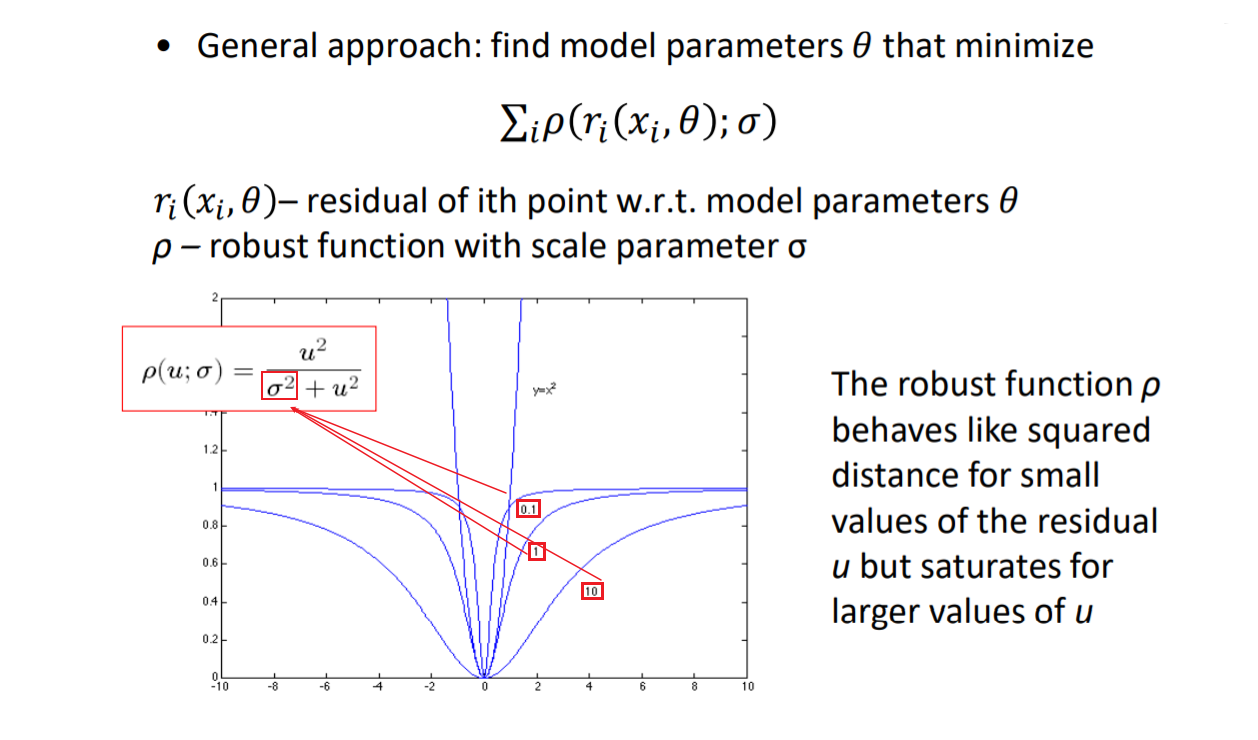
- 鲁棒函数估计
- 对于一个非线性的优化问题就不能使用前面的方程求解，需要使用迭代的方式求解类似于梯度下降
- 先不考虑鲁棒拟合的问题，利用最小二乘得到一个初始解
- 根据经验将尺度参数$\sigma$设置成$1.5$倍的平均残差
- 处理后的效果
3.2 RANSAC（随机采样一致性）
当存在许多的点都不在模型上，或者是图片被遮挡，这种时候就需要使用较少的点来拟合出模型
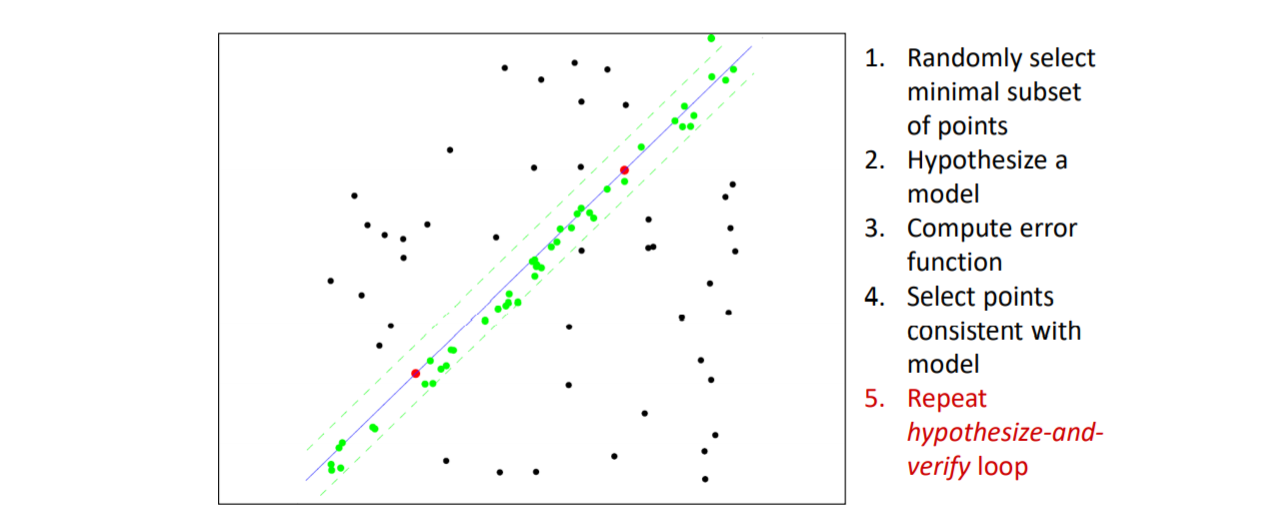
- RANSAC
- 选择一个最小的集合$s$（估计一条直线需要两个点）
- 拟合出一个模型
- 设置一个门限$t$
- 用门限$t$内剩余的点给这个模型“投票”，即“离得近”就 得分
- 重复上述过程，取“得分”最高的模型,设置迭代次数$N$
- 选择参数
$e$：外点率，$s$：模型的最小范围，$N$：最大迭代次数，$p$：正确率
-
自适应的参数提取 在实际问题中，只知道参数$t,s$,无法知道外点率$e$也就无法确认迭代次数$N$。 解决方法如下：
-
使用RANSAC思想进行指纹识别
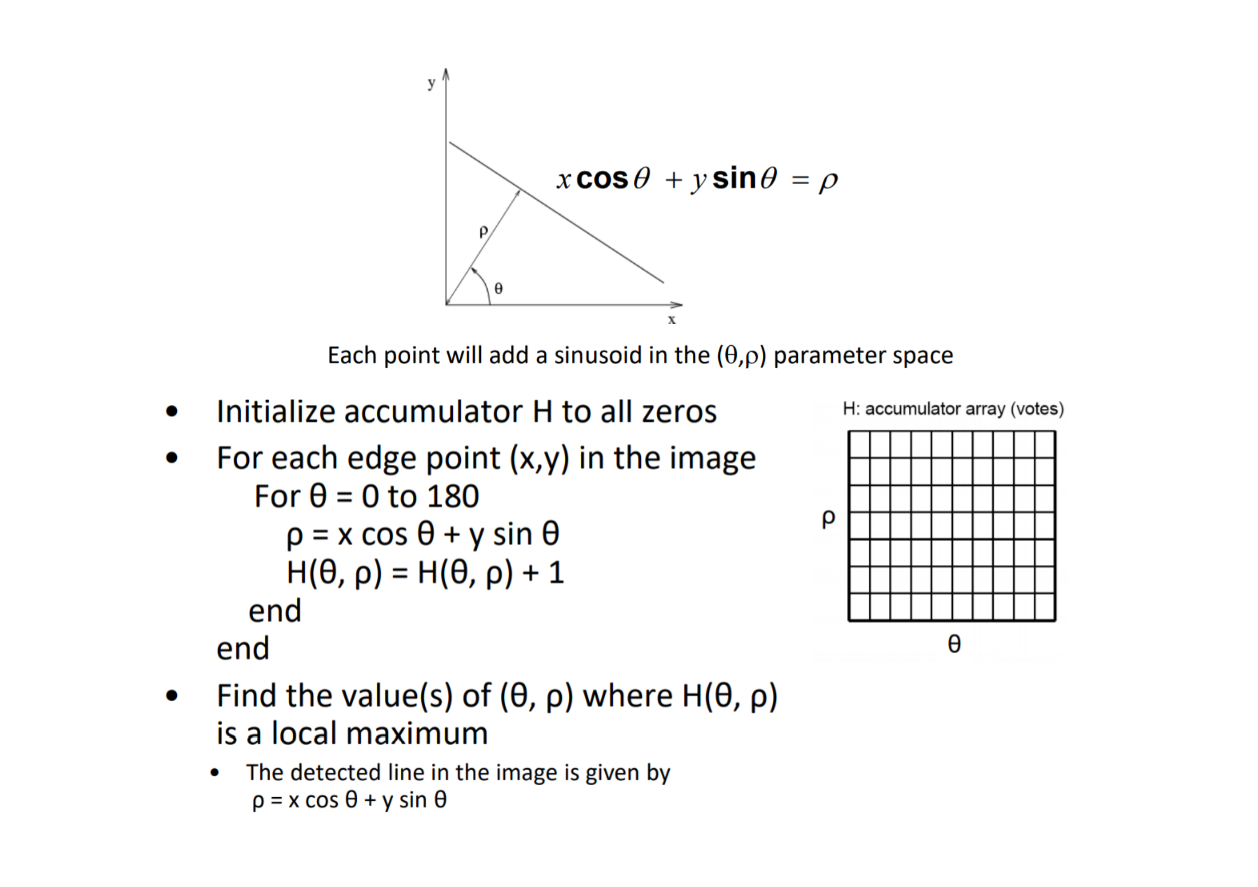
4 霍夫变换（Hough Transfrom）
于对存在大量的线的模型，即使设置了较小的门限也无法有效的区分“谁是谁的内点”
主要的改进策略：将点不在是对某一条直线投票，将投票离散化，使图像空间对参数空间进行转换
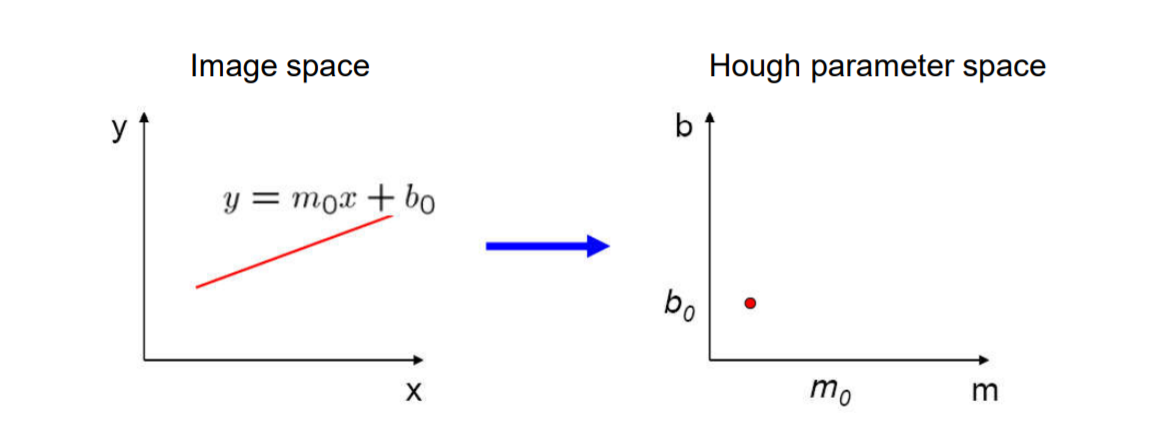
图像空间的一条直线在参数空间是一个点，参数空间多条线的交点是图像空间的边
如果使用直角坐标那么参数范围不好界定，穷举就很困难，例如当图像空间的一条竖直方向的直线，此时$x$取定值，$y$取任意值，在参数空间中就无法表示；在训练过程中也无法给$m,b$划分范围。
使用极坐标系问题就解决了：极坐标的$\theta$可以取$[0 ,180]$，可以完整的与图像空间对应
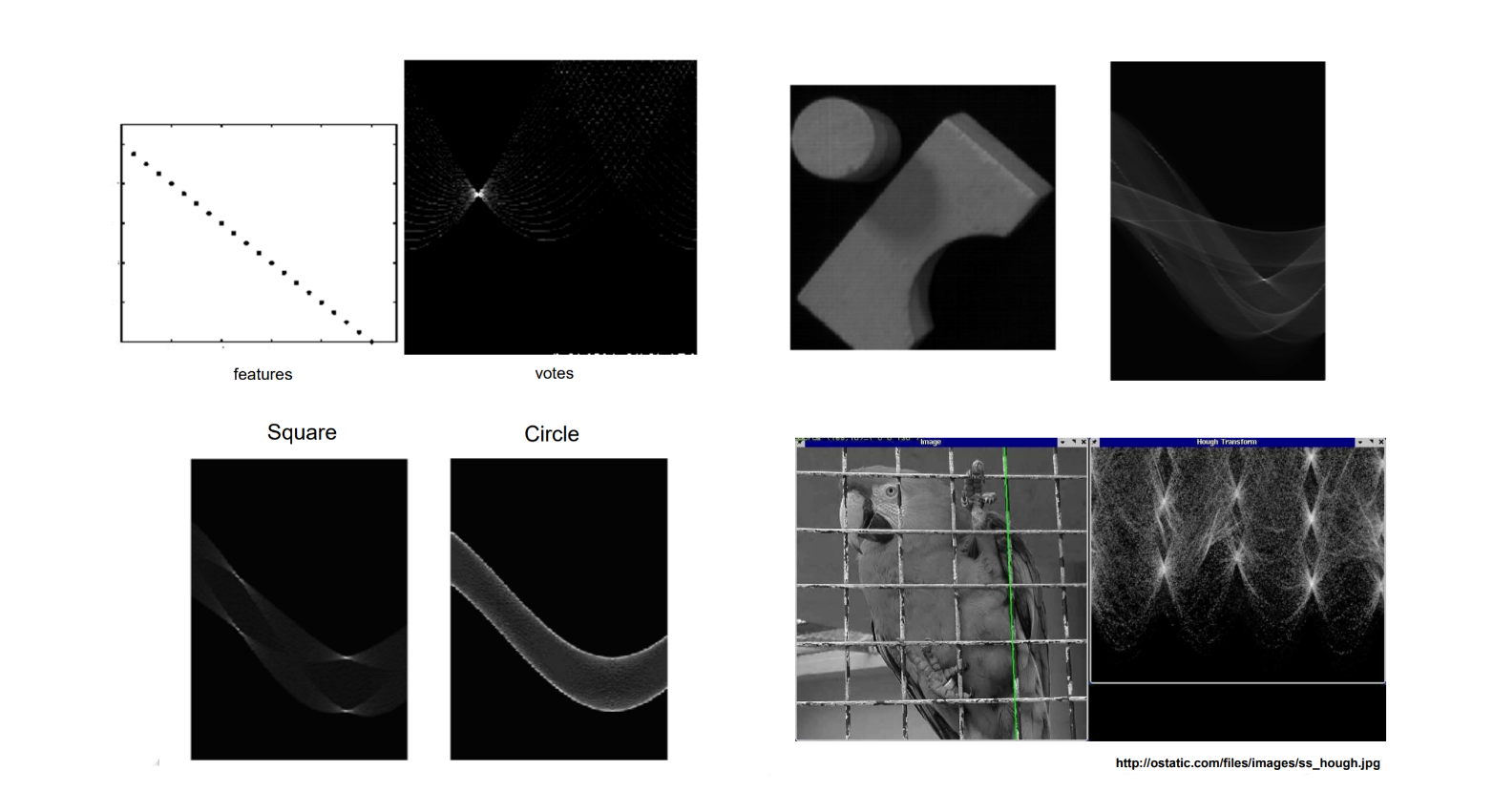
- 一些例子
-
霍夫变换处理噪声
在Candy算子中得到点时就知道了梯度方向，相应的边缘方向的范围就大概确认了，这是就是可以缩小$\theta$的范围，从而解决了噪声的影响，也简化了计算
-
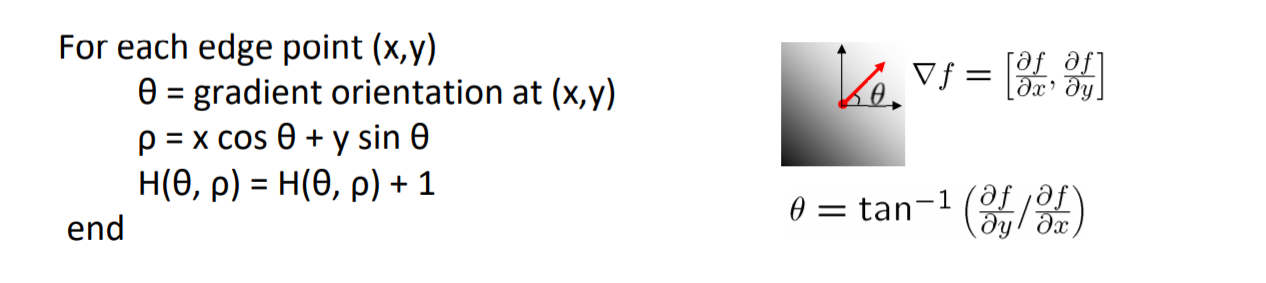
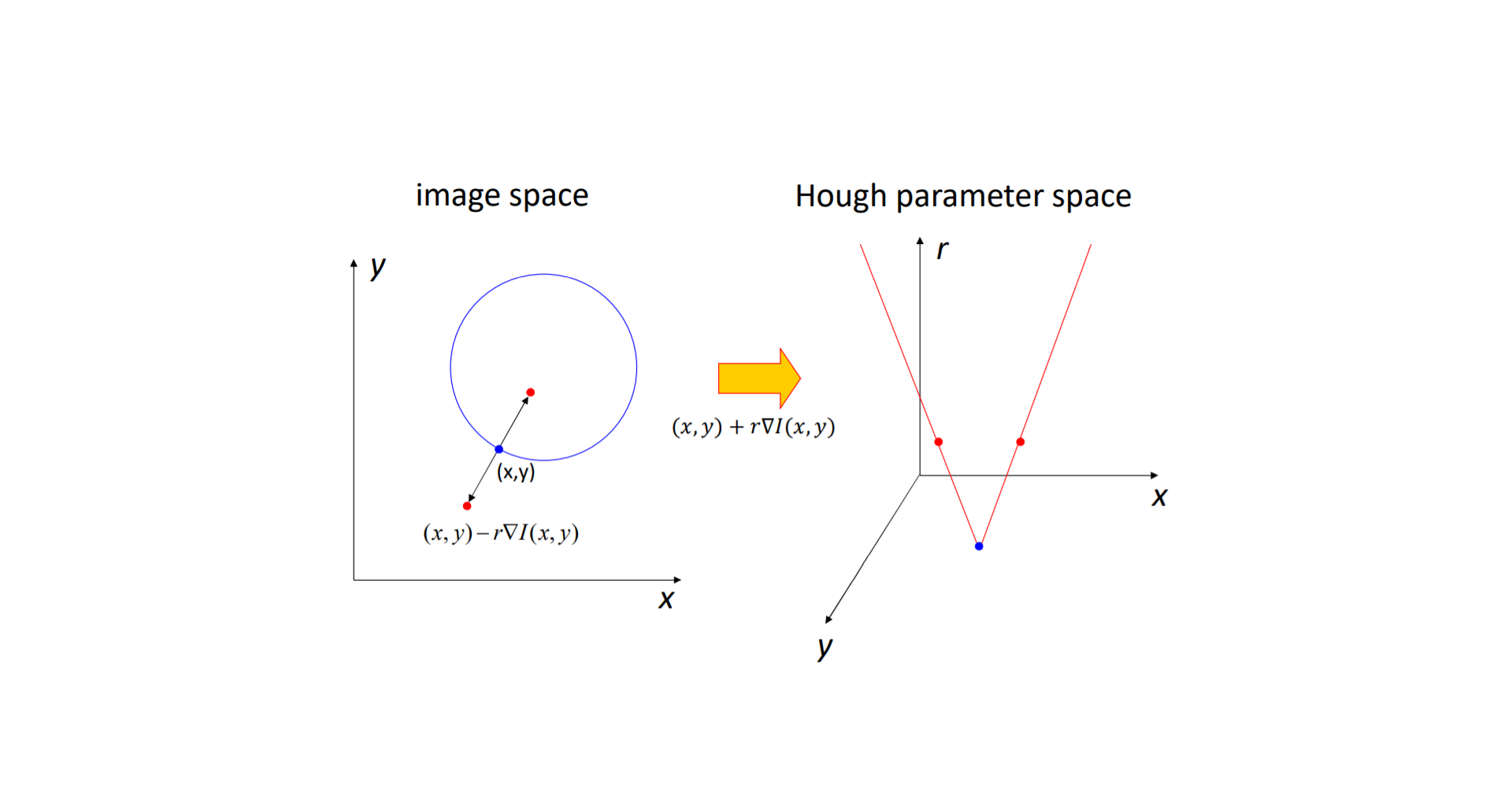
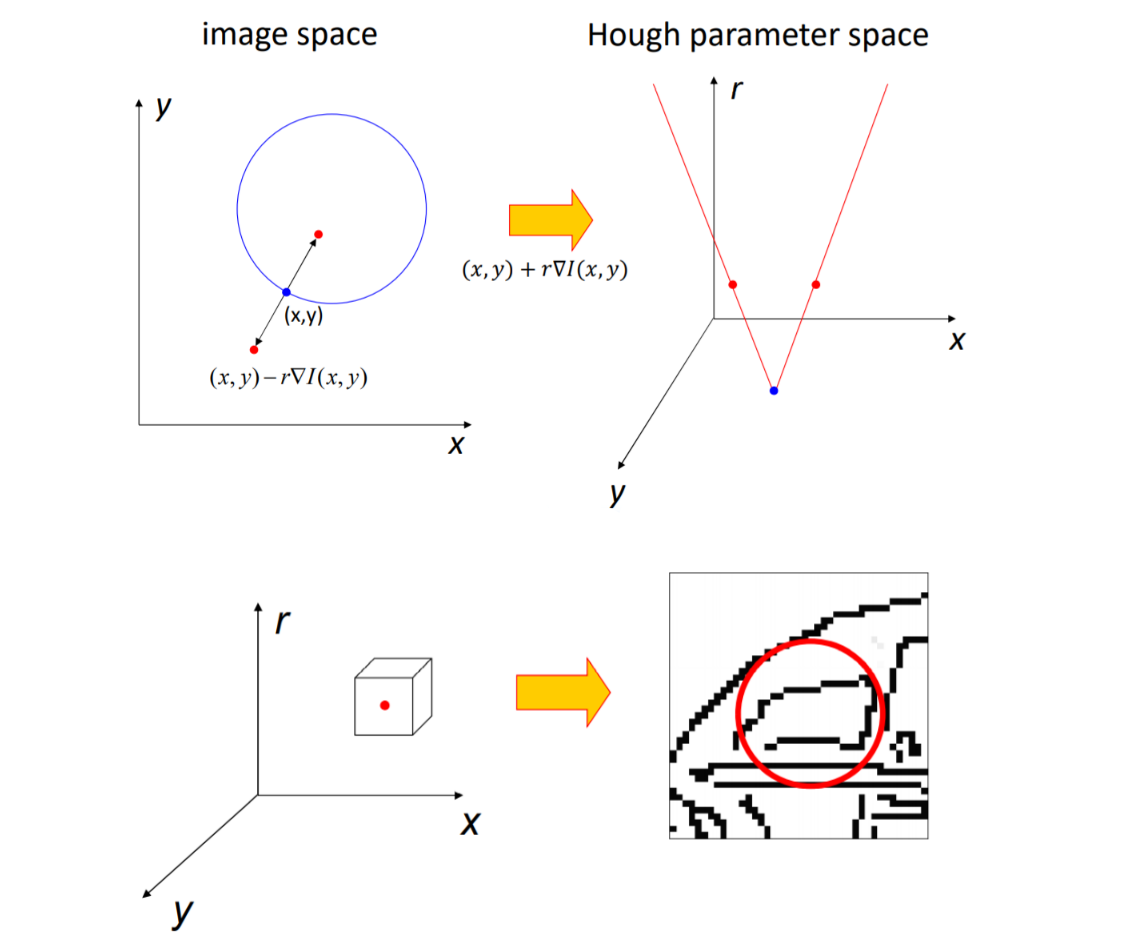
霍夫变换拟合圆
确定一个圆需要圆心坐标$(x, y)$和半径$r$，有三个参数，参数空间就需要是一个三维空间，取圆上的一个点，则可以由梯度方向确定半径方向，穷举所用的$r$(大于0，小于图像长度)，遍历圆上的点对$r$进行投票，最后在参数空间会得到一个票数高的三维空间，这个三维空间的中的一点$(x,y,r)$就可以作为拟合的圆心和半径。
学习资源：北京邮电大学计算机视觉——鲁鹏
