TensorFlow2.1入门学习笔记(6)——激活函数

0.1 常见函数

0.1.0.1 tf.where(条件语句，真返回A，假返回B)

import tensorflow as tf
a = tf.constant([1, 2, 3, 1, 1])
b = tf.constant([0, 1, 3, 4, 5])
# 若a>b，返回a对应位置的元素，否则返回b对应位置的元素
c = tf.where(tf.greater(a, b), a, b)  
print("c：", c)		# c： tf.Tensor([1 2 3 4 5], shape=(5,), dtype=int32)

0.1.0.2 np.random.RandomState.rand(维度)

返回一个[0, 1)之间的随机数

import numpy as np
rdm = np.random.RandomState
a = rdm.rand()		# 返回一个随机标量
b = rdm.rand(2,3)	# 返回一个维度为2行3列的随机数矩阵
print("a:",a)		# a: 0.417022004702574
print("b:",b)		# b: [[7.20324493e-01 1.14374817e-04 3.02332573e-01][1.46755891e-01 9.23385948e-02 1.86260211e-01]]

0.1.0.3 np.vstack(数组1，数组2)

将两个数组按垂直方向叠加

import numpy as np
a = np.array([1,2,3])
b = np.array([4,5,6])
c = np.vstack(a,b)
print("c:",c)		# c:[[1 2 3][4 5 6]]

0.1.0.4 np.mgrid[]

np.mgrid[起始值 : 结束值 : 步长，起始值 : 结束值 : 步长, ……] 包含起始值，不包含结束值

0.1.0.5 x.ravel()

x.ravel() 将x变为一维数组，将变量拉直

0.1.0.6 np.c_[]

np.c_[数组1，数组2，……] 使返回的间隔数值点配对

0.1.0.6.1 例：

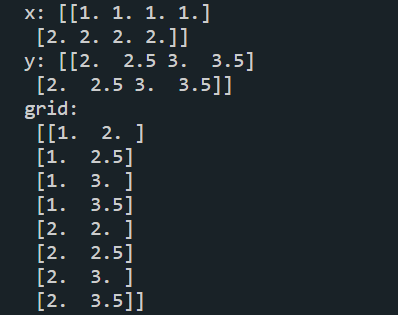
import numpy as np
x, y = np.mgrid[1:3:1,2:4:0.5]
grid = np.c_[x.ravel(),y.ravel()]
print("x:",x)
print("y:",y)
print("grid:\n",grid)

运行结果：

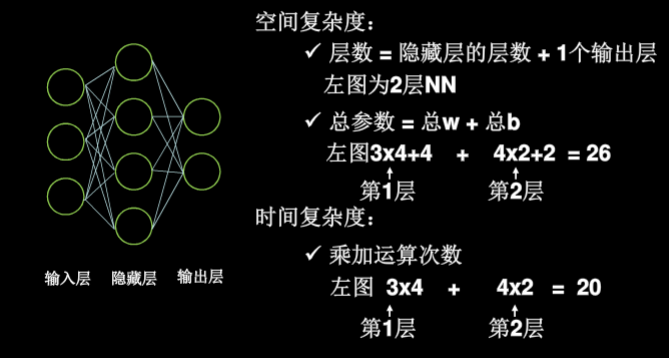
0.2 神经网络（NN）复杂度

• NN复杂度：用NN层数和NN参数的个数表示
• 空间复杂度：层数 = 隐藏层的层数 + 1个输出层
• 总参数：总w数 + 总b数
• 时间复杂度：乘加运算次数

0.3 学习率

选择合适的学习率来更新参数

• 指数衰减学习率 $指数衰减学习率 = 初始学习率*学习率衰减率^\frac{当前层数}{多少轮衰减一次}$

import tensorflow as tf

w = tf.Variable(tf.constant(5, dtype=tf.float32))

epoch = 40
LR_BASE = 0.2  		# 最初学习率
LR_DECAY = 0.99  	# 学习率衰减率
LR_STEP = 1			# 喂入多少轮BATCH_SIZE后，更新一次学习率

for epoch in range(epoch):  # for epoch 定义顶层循环，表示对数据集循环epoch次，此例数据集数据仅有1个w,初始化时候constant赋值为5，循环100次迭代。
    lr = LR_BASE * LR_DECAY ** (epoch / LR_STEP)
    with tf.GradientTape() as tape:  	# with结构到grads框起了梯度的计算过程。
        loss = tf.square(w + 1)
    grads = tape.gradient(loss, w)  	# .gradient函数告知谁对谁求导

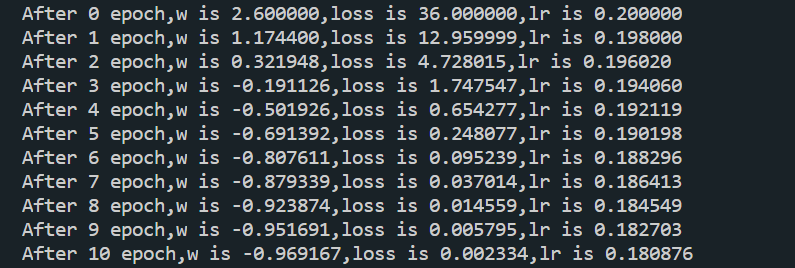
    w.assign_sub(lr * grads) 			# .assign_sub 对变量做自减 即：w -= lr*grads 即 w = w - lr*grads
    print("After %s epoch,w is %f,loss is %f,lr is %f" % (epoch, w.numpy(), loss, lr))

运行结果：

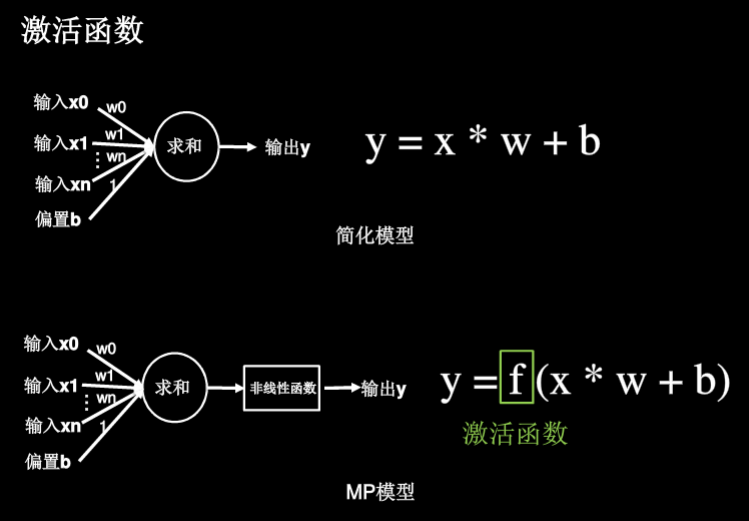
0.4 激活函数

简化模型始终是线性函数，影响模型的表达力 MP模型多了一个非线性函数（激活函数），使得多层神经网络不再是线性，提高层数来提高模型表达力

0.4.0.7 好的激活函数的特点：

• 非线性：激活函数非线性时，多层神经网络可以逼近所有函数
• 可微性：优化器大多用梯度下降更新参数
• 单调性 ：当激活函数是单调的，能保证单层神经网络的损失函数是凸函数（更容易收敛）
• 近似恒等性：$f(x)\approx x$当参数初始化为随机小值时，神经网路更稳定

0.4.0.8 激活函数输出值的范围：

• 激活函数为有限值时，基于梯度下降的优化方法更稳定
• 激活函数输出为无限值时，可调小学习率

0.4.0.9 常用的激活函数

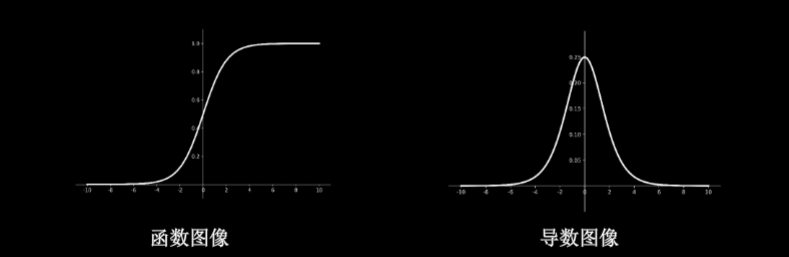
0.4.0.9.1 Sigmoid函数：tf.nn.sigmoid(x)

$f(x)=\frac{1}{1+e^{-x}}$

• 特点:

1. 易造成梯度消失
2. 输出非0均值，收敛慢
3. 幂运算复杂，训练时间长

• 函数图像

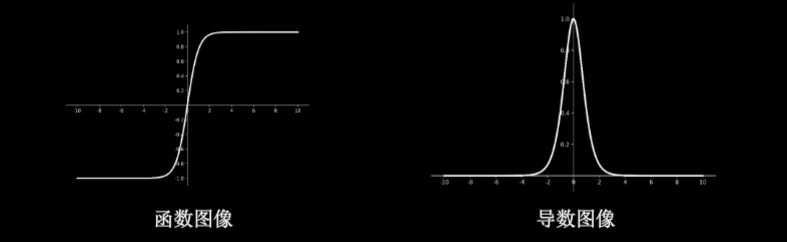
0.4.0.9.2 Tanh函数：tf.math.tanh(x)

$f(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$

• 特点

1. 输出是0均值
2. 易造成梯度消失
3. 幂运算复杂，训练时间长

• 函数图像

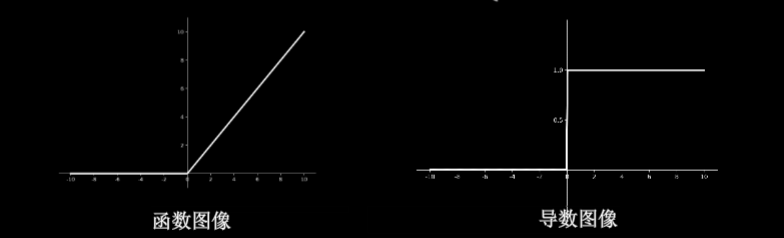
0.4.0.9.3 Relu函数：tf.nn.relu(x)

$f(x)=max(x,0)$

• 优点

1. 解决了梯度消失问题（在正区间内）
2. 只需判断输入是否大于0，计算速度快
3. 收敛速度远快于sigmoid和tanh

• 缺点

4. 输出非0均值，收敛慢
5. Dead Relu问题：某些神经元可能永远不会被激活，导致相应的参数不能被更新

• 函数图像

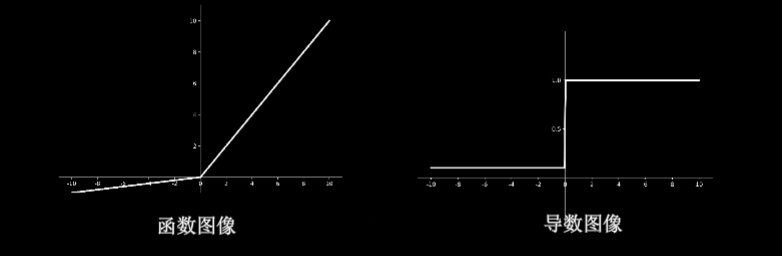
0.4.0.9.4 Leaky Relu函数：tf.nn.leaky_relu(x)

$f(x)=max(\alpha x,x)$

• 特点：理论上来说，Leaky Relu有Relu的所有优点，也不会出现Dead Relu问题，但是在实际使用过程中，并没有完全证明比Relu好用
• 函数图像

0.4.0.9.5 SUMMARIZE

• 首选relu函数
• 学习率设置较小值
• 输入特征标准化，即让输入特征满足以0为均值，1为标准差的正态分布
• 初始化中心化，即让随机数生成的参数满足以0为均值，$\sqrt{\frac{2}{当前输入特征个数}}$为正态分布

主要学习的资料，西安科技大学：神经网络与深度学习——TensorFlow2.0实战，北京大学：人工智能实践Tensorflow笔记