基于纹理的复杂环境下道路消失点检测算法

| 标题 | 基于纹理的复杂环境下道路消失点检测算法 |
|---|---|
| 年份: | 2014 年 6 月 |
| GB/T 7714: | [1]傅重添, 杨健, 路飞飞. 基于纹理的复杂环境下道路消失点检测算法[J]. 计算机应用与软件, 2014(6):292-294. |
1 摘要
在乡村或者越野环境中,道路没有明显的边界和行车线,阻碍了一般视觉道路检测算法的应用。采用计算道路消失点的 方法,提出一种快速的局部适应软投票 FLASV( Fast Local Adaptive Soft Voting) 算法。算法首先采用 Gabor 滤波器计算每个像素点的 纹理方向,然后依据像素点的置信水平决定是否参与投票,最后采用快速局部投票的算法估计消失点的位置。实验结果分析表明,该算法能很好地适应复杂多变的环境,具有较低的时间复杂度和较高的准确性。
2 研究方法
2.1 1. 纹理方向估计
图像纹理分析方法大致分为基于传统的方法,基于纹理模型的方法和基于信号变换的方法。
基于 Gabor 滤波器 的纹理分析法是一种基于信号变换的空域—频域联合分析的方 法,它克服了传统傅里叶方法的不足,能很好地兼顾信号在频率 域和空间域中的分辨能力,具有在空间域和频率域能够同时取 得最优局部化的特性,因而在理论上具有比其他方法更好的纹 理区分能力。
基于多尺度多方向的Gabor滤波器的变换函数表达式为:
$$ \psi_{\omega, \varphi}(x, y)=\frac{\omega}{\sqrt{2 \pi} c} \mathrm{e}^{\frac{-\omega^{2}\left(4 a^{2}+b^{2}\right)}{\left(8 c^{2}\right)}}\left(\mathrm{e}^{\mathrm{ia\omega}}-\mathrm{e}^{\frac{-c^{2}}{2}}\right) $$
式中,$\omega$和 $\phi$表示尺度和方向。本文使用 36 个方向,5 个尺度 的 Gabor 滤波器,即$\omega$ = 5,$\phi$= 36,$a = xcos\phi+ ysin\phi,b = - xsin\phi+ ycos\phi,c = 2.2$。
对图像和 Gabor 滤波器进行卷积操作,令 $I( x,y) $表示图像 在点$ (x,y)$ 处的灰度值,卷积操作表示为: $\zeta_{\omega, \phi}=I \otimes \psi_{\omega, \phi}$
卷积的结果 $\zeta_{\omega, \phi}$在点 $z = ( x,y)$ 处有两部分: 实部和虚部,定义$R_{\phi}(z)$为$z$点处某一尺度和方向上的响应值,则: $R_{\phi}(z)=\operatorname{average}_{\omega}\left(\operatorname{Re}\left(\zeta_{\omega, \phi}\right)^{2}+\operatorname{lm}\left(\zeta_{\omega, \phi}\right)^{2}\right)$
$R_{\phi}(z)$的最大值为$z=(x,y)$处的纹理方向$\theta(z)$,其中$\theta(z) = argmax_{\phi}R_{\phi}(z)$
覆盖在图像上的线段表示的方向就是该像素 点的纹理方向
2.2 2. 置信水平估计
有Gabor方法虽然得到了图像中每个像素点的纹理方向,但不能保证每个方向都是正确的,因此引入当置信水平概念,当置信水平大于一定阈值,则认为是投票点。由于某一像素点有 36 个方向的响应值,令 $r_1( z) > … > r_{36} ( z)$ 表示响 应值从大到小排序( 显然 $r_1(z) = R_{\theta(z)}( z) )$ ,像素点 $z = ( x,y)$)处 的置信水平定义为: $$ \operatorname{Conf}(z)=1-\frac{\text { Average }\left(r_{5}(z), \cdots, r_{15}(z)\right)}{r_{1}(z)} $$
实验中,令阈值为$\eta = 0.4 × ( max_z Conf(z)-min_z Conf( z) )$ ,置信水平大于$\eta$的像素点为投票点。
2.3 3. 快速局部投票算法
在得到了每个像素点的纹理方向和可信像素之后,就可以通过投票算法来估计消失点的位置。
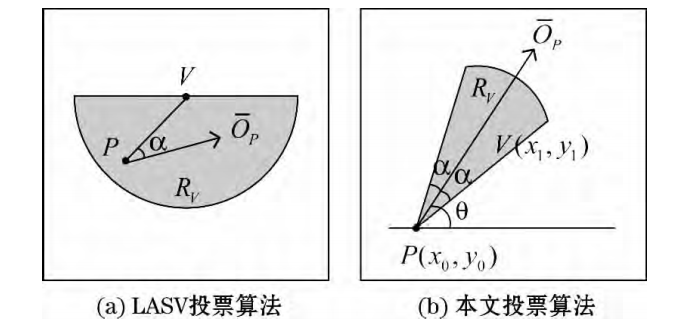
H.Kong等提出的LASV投票算法如图(a):对于图像中每一个候选消失点$V$,它的投票区域 $R_V$是以 $V$ 为圆心,半径为 $r = 0.3H$( $H$ 是图像的高度) 的下半圆,投票区域中的某一点$P$的纹理方向为 $\vec{OP}$,若线段$PV$和$P$点纹理方向之间的夹角$∠( PV,O_p)$ 小于某一个阈 值 $α$,则对 $V$ 点投票,投票过程表示为:
式中,$γ$ 表示线段$PV$和 $P$ 点的纹理方向 $\vec{O_P}$之间的夹角,$d( P,V)$ 表示点 $P$ 和 $V$ 之间的距离。该算法的缺点是时间复杂度高,为 $O( n^3 )$ ,主要原因是它将图像中的每一个像素点都作为候选消失点,然后搜索其投票区域$R_V$,并执行投票算法。
置信水平大于 η 的投票点个数远远小于候选消失点的个 数,可以用投票点来找消失点,这样只需遍历一遍投票点,而不 用搜索整个候选消失点,据此,本文提出了一种快速局部投票算法( FLASV) 。如图 ( b) 所示,对于图像中某一投票点 P,该点 的纹理方向为$\vec{O_p}$,本文的投票区域$R_V$是以 P点为圆心,半径为 r = 0.3H( H 为图像的高度) ,顶角为 2α 的扇形区域,则点P向 投票区域 RV中的所有像素点投票,投票过程表示为:
式中,$d( P,V)$ 表示点 P 和 V 之间的距离,β 表示线段PV和 P 点的纹理方向之间的夹角,根据经验,正常图像中道路消失点的位置不会在图像边缘,故本文对于边缘像素不做处理,
该算法的步骤:
- Step1 构造一个与图像大小一致的矩阵M,矩阵初始化为0;
- Step2 对于每一个投票点 $P(x_0,y_0 )$ ,其对应的投票区域 为 $R_V$,对于任意点 $V(x_1,y_1)∈R_V,M(P,V) = M(P,V) + exp(-β×d(P,V))$ ,其中 $β = \angle( PV,O_P ),d( P,V) = sqrt( ( x_1 - x_0 )^2 + ( y_1 - y-0 )^2 ) ;$
- Step3 输出矩阵 M 中最大值的位置即为图像中道路消失点的位置
3 实验与结果分析
- 实验数据集:选取了 575 幅非结构化道路 图片进行验证,图片包括在沙漠、草地、雪地等多种复杂环境,还 包括不同的光照以及车辆、行人等运动物体的干扰。
- 实验配置:操作系统:Windows 7,软件环境:Matlab 2011b,硬件环境为: Intel Core i3 CPU( 2.53GHz) ,DDR3-4GB内存,图像大小为 240 × 180。
通过实验分析比较,说明该算法不仅能够准确检测到复杂环境下的道路消失点,而且大大降低了算法的时间复杂度