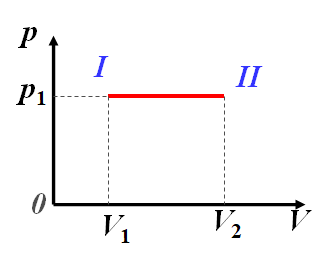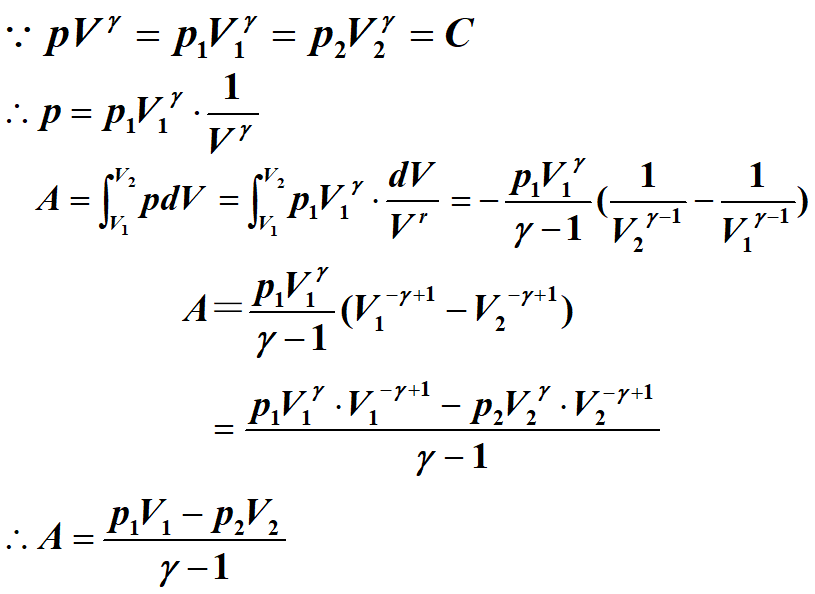热力学第一定律 等值过程 绝热过程

1 热力学第一定律
1.1 内能,功和热量
-
实际气体内能:所有热分子热运动的动能和分子势能的总和
-
内能是状态量: $E=E(T,V)$
理想气体内能: $E={\frac{M}{M_{mol}}{\frac{i}{2}}RT}$
是状态参量T的单值函数
-
系统内能改变的两种方式
- 做工可以改变系统的状态:摩擦升温(机械功),电加热(电功)
- 热量的传递可以改变系统的内能:热量是过程量
1.2 准静态过程
- 准静态过程:系统从一个平衡态到另一个平衡态,如果过程中所有的中间态都可以近似的看作平衡态法过程
- 准静态过程是理想化过程
弛豫时间$\tau$: 系统从一个平衡态变道相邻平衡态所经过的时间
当$\Delta t_{过程}»\tau$: 过程就可以视为准静态过程,故 无限缓慢 只是一个相对的概念。
非静态过程: 系统从一平衡态到另一平衡态,过程中所有中间态为非静态的过程
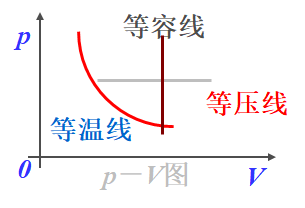
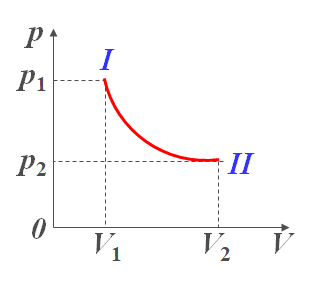
- 准静态过程曲线
p-V图上,一个点代表一个平衡态,一条连续的曲线代表一个准静态过程
1.3 准静态过程的功与热
1.3.1 体积功:
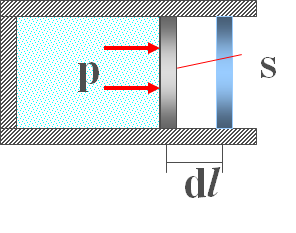
当活塞移动微小位移$dl$时,系统外界所做的元功为:
$$dA = Fdl = pSdl = pdV$$
$$A=\begin{aligned}\int_{V_{1}}^{V_{2}} p \mathrm{d} V\end{aligned}$$
$dV>0,dA>0$系统对外界做正功
$dV<0,dA<0$系统对外界做负功
$dV=0,dA=0$系统不做功
- 功是过程量
- 做功改变系统热力学状态的微观实质
-功是系统与外界交换的能量的量度
1.3.2 准静态过程中的热量计算
$$C = \frac{dQ}{dT}$$
C(热容量):系统在某一无限小过程中吸收热量$dQ$与温度变化$dT$的比值 单位:$J\cdot K^{-1}$
热容量与比热的关系为:$C = Mc_{比}$
$C_m$(摩尔热容量):
$$C = {\frac{M}{M_{mol}}}{C_{m}}$$
$$dQ = {\frac{M}{M_{mol}}}{C_m}{dT}$$
$$Q = {\frac{M}{M_{mol}}}{C_m}(T_2-T_1)$$
- 传热的微观本质:
- 热量也是能量变化的量度
1.4 热力学第一定律
对于任一过程,系统与外界可能同时有功和热量的转换,且系统能量改变仅为内能时,根据能量守恒: $$\Delta E = Q + (-A)$$
或$$Q = \Delta E + A$$
-
$Q>0$系统吸热,$Q<0$系统放热
-
$A>0$系统对外做功,$A<0$外界对系统做功
-
$\Delta E> 0$系统内能增加,$\Delta E<0$系统内能减少
-
如果系统经历一些微小变化过程,则$dQ=dE+dA$;
-
对准静态过程:
$$dQ=dE+pdV$$
$$Q=\Delta E + {\begin{aligned}{\int_{V_{1}}^{V_{2}}}p{\mathrm{d} V}\end{aligned}}$$
2 理想气体等值过程
2.1 等容过程,定容摩尔热容
$$\because dV=0,dA= pdV = 0$$
$$\therefore dQ=dE={\frac{M}{M_{mol}}}{\frac{i}{2}}RdT$$
$$Q_V=E_2-E_1={\frac{M}{M_{mol}}}{\frac{i}{2}}Rd(T_2-T_1)$$
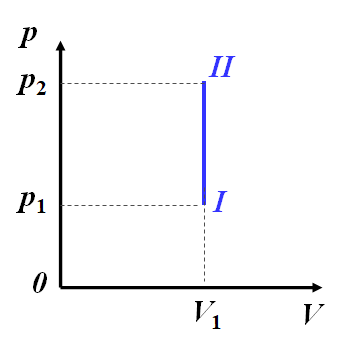
定容摩尔热容量
-
单原子理想气体:$C_{V,m}={\frac{3}{2}}R$
-
双原子理想气体:$C_{V,m}={\frac{5}{2}}R$
-
多原子理想气体:$C_{V,m}=3R$
理想气体内能 $$E={\frac{M}{M_{mol}}}{C_{V,m}}T$$ 理想气体的任一$T_1\rightarrow T_2$过程 $$dE=\nu C_{V,m}dT$$ $$\Delta E=E_2-E_1={\nu}{\begin{aligned}{\int_{T_{1}}^{T_{2}}}{C_{V,m}}{\mathrm{d} T}\end{aligned}}$$ 若$C_{V,m}$近似为常数,则有$\Delta E = \nu C_{V,m}\Delta T$
2.2 等压过程,定压摩尔热容
$$dA=pdV$$ $$dQ_p=dE+pdV$$ $$A_p={\begin{aligned}{\int_{V_{1}}^{V_{2}}}p{\mathrm{d} V}\end{aligned}}=p(V_2-V_1)$$ $$Q_p={\frac{M}{M_{mol}}}{\frac{i}{2}}R(T_2-T_1)+{\frac{M}{M_{mol}}}R(T_2-T_1)$$
定压摩尔热容量 $$dQ_p=dE+dA_p=C_{V,m}dT+pdV$$ $$pV=RT微分得pdV=RdT$$ $$dQ_p={\frac{i}{2}}R\cdot dT+R\cdot dT$$ $$C_{p,m}=(\frac{dQ}{dT})p$$ $$C{p,m}={\frac{i}{2}}R+R$$ $$C_{p,m}=C_{V,m}+R$$ $$Q_{p,m}={\frac{M}{M_{mol}}}{C_{p,m}}(T_2-T_1)$$
比热容比: $\gamma =\frac{C_{p,m}}{C_{V,m}}$为绝热系数
理想气体:$\gamma =\frac{C_{p,m}}{C_{V,m}}=\frac{\frac{i}{2}R+R}{\frac{i}{2}R}=\frac{i+2}{i}$
- 对单原子分子:$i=3,\gamma=1.67$
- 对刚性双原子分子:$i=5,\gamma=1.40$
- 对刚性多原子分子:$i=6,\gamma=1.33$
2.3 等温过程
$dT=0,dE=0$
$dQ_T=dA_T$
$dQ_T=pdV,p=\nu RT\cdot \frac{1}{V}$
$Q_T=A_T={\begin{aligned}{\int_{V_{1}}^{V_{2}}}\nu RT{\frac{dV}{V}}\end{aligned}}=\nu RTln{\frac{V_2}{V_1}}=p_1 V_1 ln{\frac{V_2}{V_1}}$
2.4 绝热过程
系统变化过程中,系统与外界没有热交换
- 特征:$dQ=0,dE+dA=0$
2.4.1 绝热方程
-
对于准静态方程 $\nu C_{V,m}dT+pdV=0$
$pV=\nu RT$
取微分得
$pdV+Vdp=\nu RdT$
消去$\nu dT$得
$pdV+Vdp=-R{\frac{pdV}{C_{V,m}}}$
${C_{V,m}}pdV+{C_{V,m}}Vdp=-RpdV$
${C_{p,m}}pdV+{C_{V,m}}Vdp=0$
${\frac{dp}{p}}+\gamma {\frac{dV}{V}}=0$
积分得
${\begin{aligned}\int \frac{dp}{p}\end{aligned}}+{\begin{aligned}\int \gamma \frac{dV}{V}\end{aligned}}=0$
得
$lnp+\gamma lnV=C$
$lnpV^\gamma=C$
$pV^\gamma=C_1$
$pV^{\gamma-1}=C_2$
$p^{\gamma-1}T^{-\gamma}=C_3$,即松柏方程
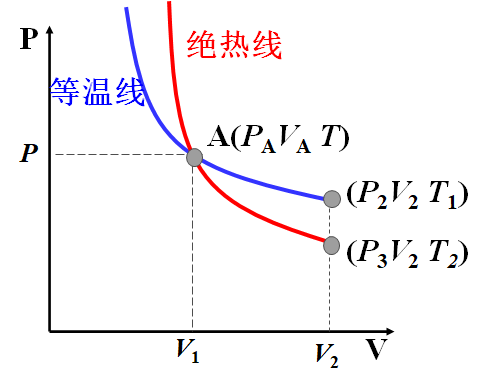
2.4.2 绝热线与等温线
$pV=C_1,等温线$
$pV^\gamma=C_2,绝热线$
-
对于等温过程
$pV=C_1=p_A V_A$
$p=\frac{C_1}{V}$
$\frac{dp}{dV}|_{AT}=-\frac{C_1}{V^2}|_A=-\frac{C_1}{V_A ^2}=-\frac{p_AV_A}{V_A ^2}=-\frac{p_A}{V_A}$
-
对于绝热过程
$pV^\gamma=C_2=p_AV_A ^\gamma$
$p=\frac{C_2}{V^\gamma}$
$\frac{dp}{dV}|_{A\gamma}=-\gamma \frac{C_2}{V^{\gamma+1}}|_A=-\gamma \frac{p_AV_A ^\gamma}{V_A ^{\gamma+1}}=-\gamma \frac{p_A}{V_A}$
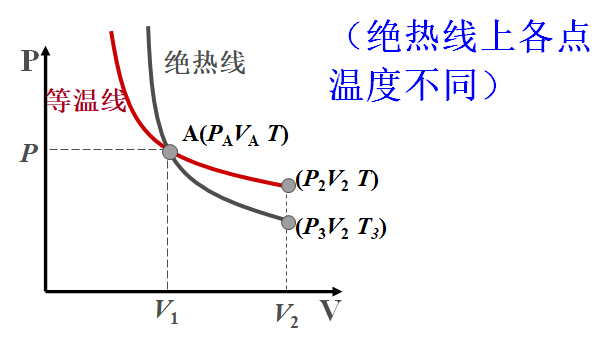
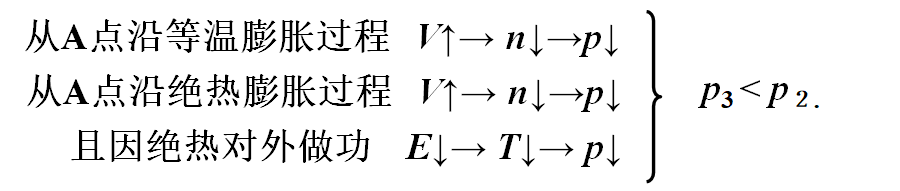
$\because \gamma > 1$
$\therefore |\frac{dp}{dV}|{A\gamma}=\gamma \frac{p_A}{V_A}>|\frac{dp}{dV}|{AT}=\frac{p_A}{V_A}$
即绝热线要陡一些
$p=nkT$