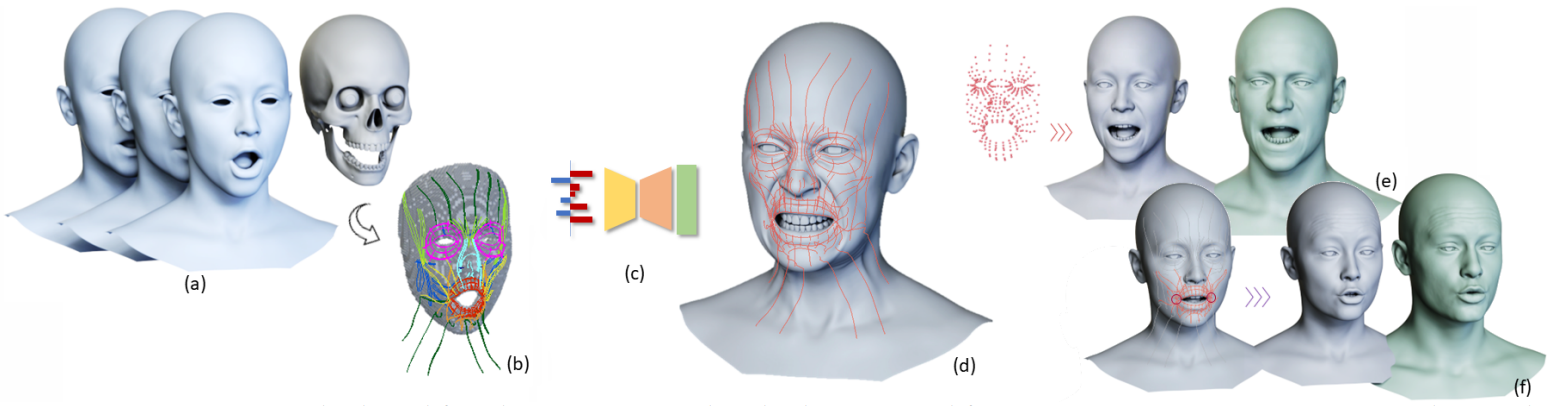
Animatomy: an Animator-centric, Anatomically Inspired System for 3D Facial Modeling, Animation and Transfer
| Animatomy: an Animator-centric, Anatomically Inspired System for 3D Facial Modeling, Animation and Transfer | |
|---|---|
| 年份: | 2022 年 11 月 |
| GB/T 7714: | Choi B, Eom H, Mouscadet B, et al. Animatomy: an Animator-centric, Anatomically Inspired System for 3D Facial Modeling, Animation and Transfer[C]//SIGGRAPH Asia 2022 Conference Papers. 2022: 1-9. |
1 介绍
提出了一种基于面部肌肉曲线的解刨学面部捕捉系统,该技术应用于《阿凡达:水之道》
相关工作
-
相比于
Blendshapes和Facial Rigging,该方法- 使用
178个参数拟合面部动作 - 使用肌肉模拟来拟合一个新的的动态面部扫描语料库,可以直接使用笔刷修改
- 肌肉曲线是
skeletal rigging的一种变形
- 使用
-
基于
Data-driven和Morphable Models的方法- 构建出了基于肌肉张力的表情变化和皮肤变形模型
-
基于
Muscle-based Physical Model扫描的方法- 使用该方法构建了一个数据集
2 系统设计
目标
-
Artistic Control:可编辑
-
Anatomically Grounded Representation:捕获肌肉模拟行为进行有效的
运动学控制 -
Data-driven Workflow:端到端的自动化人脸表示系统,优化输入数据
-
Transferable Animation:动画迁移
3 数据准备

使用机器学习方法构建面部模型,需要有相应的actor meshes, joint transformations, simulated muscle fibers构建一个面部绑定模型。
Actor Dynamic Scans
使用 3DF ZEPHYR 重建面部 3D shapes
使用 Acquiring the Reflectance Field of a Human Face 扫描,数据集包括80个动作切片(约7000帧,FACS+emotions)
使用 R3DS Wrap 获得对齐的mesh序列
通过 Rigid Stabilization of Facial Expressions 去除头部运动
Eyes and Jaw Alignment
使用非线性rig An Empirical Rig for Jaw Animation 解决下颌骨运动,并通过最小二乘优化将 jaw rig 拟合到 mesh 序列
Actor Dynamic Muscle Simulation
首先创建一个静止状态下的四面体 volume(135K),与 Phace: Physics-Based Face Modeling and Animation 类似
然后对整个扫描序列进行被动的准静态模拟,其中皮肤顶点和头骨作为四面体元素的位置约束 Loki: a unified multiphysics simulation framework for production
通过计算获得重心,将重心嵌入到肌肉曲线控制点中,对于每个模拟帧,使用它们的重心坐标来提取模拟肌肉曲线
4 解剖学面部建模
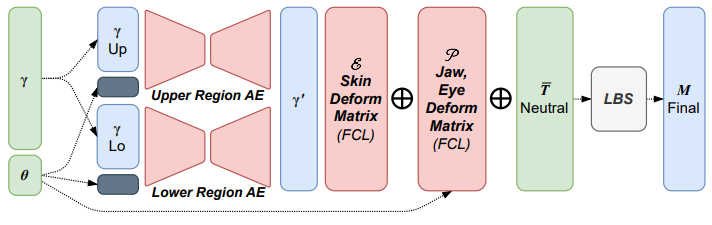
基于FLAME,顶点数 $N = 85000$ ,骨骼数 $K=3$(包括眼睛,下巴),公式如下: $$ M(\vec{\theta}, \vec{\gamma}):\R^{\vert{\vec{\theta}\times \vec{\gamma} \vert}} \to \R^{3N} $$ 表示了由位姿(眼睛,下巴)和表情到面部 $N$ 个顶点的映射,其中 $\vec{\theta} \in \R^{\vert{\vec{\theta}\vert}}$ 是位姿参数,$\vec{\gamma}\in \R^{\vert{\vec{\gamma}\vert}}$ 是表情参数
该模型如下图:
-
结合了静止(neutral)状态下的 mesh $\bar{T} \in \R^{3N}$ ,用于修正静止状态下的位姿$\vec{\theta^*}$,可以矫正**LBS(linear blend skinning)**无法修正的位姿 blendshapes $B_P(\vec{\theta}, \mathcal{P}):\R^{\vec{|\theta|}} \to \R^{3N}$
-
肌肉特征 blendshapes $B_M(\vec{\theta}, \mathcal{E}):\R^{\vec{|\gamma|}} \to \R^{3N}$ ,用于捕获面部表情
-
下颌张力自编码 $AE_{\Phi}(\vec{\theta}, \vec{\gamma}):\R^{\vec{|\gamma|}+\vec{|\theta|}} \to \R^{\vec{|\gamma|}}$ (由权重 $\Phi$ 参数化),用于加强非线性肌肉张力表现
$M$ 的公式为:
$$ \begin{aligned} & M(\vec{\theta}, \vec{\gamma})=W\left(T_P(\vec{\theta}, \vec{\gamma}), J, \vec{\theta}, \boldsymbol{\mathcal{W}}\right), \ & T_P(\vec{\theta}, \vec{\gamma})=\bar{T}+B_P(\vec{\theta} ; \mathcal{P})+B_E\left(A E_{\Phi}\left(\vec{\gamma}, \vec{\theta}_{j a w}\right) ; \mathcal{E}\right) . \end{aligned} $$
其中 $W\left(T_P, J, \vec{\theta}, \boldsymbol{\mathcal{W}}\right)$ 是 blend sking 方程 (SMPL: A Skinned Multi-Person Linear Model.),用于控制关节 $J\in\R^{3K+3}$ 周围的顶点 $T_P$ ,通过权重 $\mathcal{W}\in\R^{N \times K}$ 线性平滑
4.1 肌肉特征(张力)
肌肉曲线的长度为 $s$ ,推导出 $\gamma = (s - \bar{s})/\bar{s}$,$\bar{s}$ 为静止状态下的肌肉曲线长度。张力为肌肉静止状态下长度的偏差,正负张力对应静止状态肌肉的收缩和松弛
定义 $\Gamma = {\vec{\gamma}^{(t)}|t\leq T}$ 为肌肉张力序列,其中 $\vec{\gamma}^{(t)}$ 为第 $t$ 帧肌肉张力参数,$T$ 为总帧数
4.2 眼睛和下巴的基变
定义 $R(\vec{\theta}):\R^{|\theta|} \to \R^{9K+3}$ 表示从位姿向量 $\vec{\theta}$ (对应下巴和眼球的绑定控制)到所有相关变换矩阵的映射(其中 $\R^{3\times 3 }$ 用于眼球转动,$\R^{3\times 4 }$ 用于下巴绑定),使用 $\vec{\theta^*}$ 表示静止状态下的位姿参数,位姿 blendshape 方程定义为:
$$ B_P(\vec{\theta}, \mathcal{P})=\sum\nolimits_{k=1}^{9K+3} (R_k(\vec{\theta}) -R_k(\vec{\theta^*}))P_{k} $$
其中 $P_k\in \R^{3N}$ 为第 $k$ 个元素在 $R_k$ 作用下相关顶点的偏移,位置空间 $\mathcal{P} = [P_1, \ldots, P_{9K+3}]\in\R^{3N\times(9K+3)}$ ,包含所有的位姿 blendshapes 信息
4.3 皮肤张力变换矩阵
对皮肤张力变换矩阵进行线性 blendshapes 建模:
$$ B_E(\vec{\gamma} ; \mathcal{E})=\sum\nolimits_{i=1}^{|\vec{\gamma}|} E_i \gamma_i=\mathcal{E} \vec{\gamma} $$
其中 $\mathcal{E}=[E_1, \ldots,E_{|\vec{\gamma}|} ] \in \R^{3N\times |\vec{\gamma}|}$ 为简化后的皮肤张力变换基,$\vec{\gamma} \in \R^{|\vec{\gamma}|}$ 为张力参数,$|\vec{\gamma}|$ 为张力参数个数
4.4 张力自编码(AE)
张力自编码器通过限制张力向量在可信的面部表情边界内(expression manifold space),从而避免出现不自然的表情
主要目标是实现向表情空间的投影,构建一个有三层编码器和三层解码器的网络,在重建张力参数之前,需要将输入向量投影到隐空间,隐空间的维度是输入向量维度的一半,为有损压缩过程,由于张力向量不能直接输入到网络中,因此完全依赖全连接层(包含 $cELU$ 和 $Tanh$ 激活函数)
考虑到部分不相关的面部肌肉倾向于被一致处理,如嘴角的抽动会影响到眯眼,自编码器会倾向于将这些肌肉一起训练处理,因此需要将张力参数 $\vec{\gamma}$ 分为两部分 ,一部分是面部上区域(眼睛等)表情相关的张力参数 $\vec{\gamma_u}$ ,另一部分是面部下区域(嘴巴,下颌等)表情相关的张力参数 $\vec{\gamma_l}$ ,两个部分不相交,即 $|\vec{\gamma}| = |\vec{\gamma_u}| + |\vec{\gamma_l}|$;自编码器也对这两部分分别训练,最后将两部分张力参数合并为 ${\gamma^\prime}$
4.5 下颌建模
由于采用梯度下降方法进行建模,因此下颌绑定变换可以无限微分,使用一个易于训练和无限可微的径向基函数 (Radial Basis Function, RBF) 网络 $\chi$ 来近似建模
需要映射的下颌绑定变换是一个 6D 的向量(平移和轴角旋转),用高斯核(参数为 $\mu,\sigma$)作为 RBF 函数, 输入维度为 $\R^3$:
$$ \forall p, \mu, \sigma \in \mathbb{R}^{3 \times 3 \times 1}, g_{\mu, \sigma}(p)=\exp \left(-\sigma^{2}|p-\mu|^{2}\right) $$
给定参数 ${\psi_{i}, \mu_{i}, \sigma_{i} \mid i \leq N} \in \R^{6} \times \R^{3} \times \mathbb{R}$,数量为 $M=50$,则 RBF 网络 $\chi$ 为:
$$ \forall p \in \mathbb{R}^{3}, \chi(p)=\frac{\sum_{i=1}^{M} \psi_{i} \cdot g_{i}(p)}{\sum_{i=1}^{M} g_{i}(p)}, \text { with } g_{i}=g_{\mu_{i}, \sigma_{i}} $$
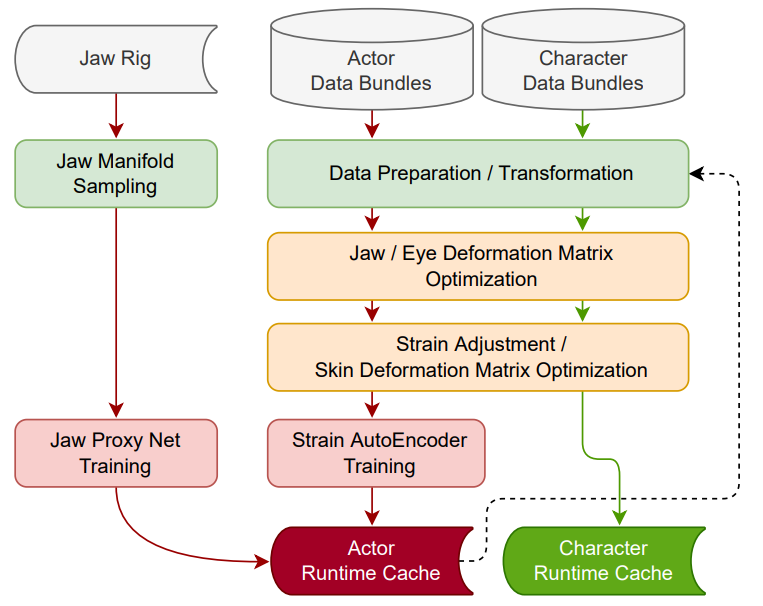
5 模型训练
模型中的参数包括:
LBS 权重:$\mathcal{W} = {\omega_{ik }} \in \R^{N \times K}$
姿态矫正 blendshape:$\mathcal{P} ={P_k | k\leq K}$
皮肤张力变换矩阵:$\mathcal{E} = {E_s | s\leq |\vec{\gamma}|}$
自编码器(AE)权重:$\Phi$
数据集共7000个,包含有 mesh $\overline{V}$ , poses $\vec{\theta}$ , strain vectors $\vec{\gamma}$
5.1 训练眼睛,下巴的权重和基础变形矩阵
训练 LBS 权重 $\mathcal{W}$ 的损失函数为:
$$ \mathcal{L}(\mathcal{W})=\sum_{t=1}^{T}\left\lVert V^{(t)}-W\left(\bar{T}, J, \vec{\theta}^{(t)}, \mathcal{W}\right)\right\rVert ^{2}+\lambda T\left\lVert \boldsymbol{W}^{(i)}-\mathcal{W}\right\rVert _{F}^{2} $$
其中 $V^{(t)} \in \R^{3N}, \vec{\theta}^{(t)}$ 为 mesh 和 pose 关于时间 $t$ 的函数,$\overline{T}$ 为初始 mesh,$J$ 为骨点位置,$W$ 为 blend sking 方程,约束条件 $0\leq\omega_{ik} \leq1$
$\mathcal{W}^{(i)}$ 由 bootstrap the iterative optimization algorithm 初始化(对模型的收敛性有极大的影响)
第二个损失项是为了避免部分骨点被激活,远离模型倾向于发生的情况
该模型为有约束的最小二乘问题,使用 CERES 算法进行优化,迭代 $50$ 轮,$\lambda = 0.1$
5.2 姿态矫正 blendshape
为进一步缩小误差,计算 $9K+3$ 个额外的姿态矫正 blendshape,损失函数为:
$$ \mathcal{L}(\mathcal{P})=\sum_{t=1}^{T}\left\lVert \hat{V}^{(t)}-\sum_{k=1}^{9 K+3}\left(R_{k}\left(\vec{\theta}^{(t)}\right)-R_{k}\left(\vec{\theta}^{*}\right)\right) P_{k}\right\rVert ^{2} $$
其中 $\mathcal{P}=\left[P_{1}, \ldots, P_{9 K+3}\right] \in \mathbb{R}^{3 N \times(9 K+3)}$ 是未知的,目标 mesh $\hat{V}^{(t)}$ 通过 blend sking 方程 $W$ 的逆变换得到
5.3 皮肤张力变换矩阵,微调张力值
将姿态矫正 blendshape 从 $\hat{V}^{(t)}$ 中移除记为 $\tilde{V}^{(t)}$,对应的张力向量记为 $\Gamma = {\vec{\gamma}^{(t)}}$,则皮肤张力变换基表示为 $\mathcal{E}=\left\lbrace E_i \right\rbrace _{i \leq |\vec{\gamma}| } \in \mathbb{R}^{3 N \times|\vec{\gamma}|}$,使用交替优化步骤计算 $\mathcal{E}$ 和 $\Gamma$,迭代 $10$ 次收敛
计算 $\mathcal{E}$ 的损失函数为:
$$ {\mathcal{L}(\mathcal{E})=\sum_{t=1}^{T}\left\lVert \tilde{V}^{(t)}-\mathcal{E} \vec{\gamma}^{(t)}\right\rVert ^{2}+\mu T \sum_{s=1}^{|\vec{\gamma}|}\left\lVert E_{s} \mathcal{D}_{s}\right\rVert _{F}^{2} .} $$
第二项为正则项,其中 $E_s$ 为一个 $3\times N$ 的矩阵(非 $\R^{3N}$ 的向量),$\mathcal{D_s}=\operatorname{diag}\left(\left[d_{s, 1}, \ldots, d_{s, N}\right]\right) \in \mathbb{R}^{N \times N}$ 为顶点,$\mu$ 表示施加于张力 $s$ 的惩罚系数,该项可以有效的避免数据污染
计算 $\Gamma$ 的损失函数为:
$$ \mathcal{L}(\Gamma)=\sum_{t=1}^{T}\left(\left\lVert \tilde{V}^{(t)}-\mathcal{\mathcal { E }} \vec{\gamma}^{(t)}\right\rVert ^{2}+\lambda\left\lVert \vec{\gamma}_{p}^{(t)}-\vec{\gamma}^{(t)}\right\rVert ^{2}\right) $$
微调时,保持 $\mathcal{E}$ 不变,只优化 $\Gamma$,从先验 $\vec{\gamma}_{p}^{(t)}$ 开始迭代,$\lambda$ 为惩罚系数
这一部分是为了更好的重建软组织的姿态(如嘴唇),当以上步骤收敛后,就可以使用 $M(\vec{\theta}, \vec{\gamma})=W\left(\bar{T}+B_{P}(\vec{\theta}, \mathcal{P}), J, \vec{\theta}, \mathcal{W}\right)$ 匹配姿态
5.4 训练张力自编码器
由两个 AE 神经网络(记为 $g_{\Phi}$ )组成,损失函数为 Euclidean L2,优化器为 LAMB,损失函数为:$\mathcal{L}(\vec{\gamma})=\left\lVert A E_{\Phi}(\vec{\gamma})-\vec{\gamma}\right\rVert$ ,自编码器表示为:
$$ AE_{\Phi}(\vec{\gamma})=g_{\Phi} (\vec{\gamma})-g_{\Phi}\left(\vec{\gamma}_{0}\right)+\vec{\gamma}_0 $$
其中 $\vec{\gamma}_0$ 为初始姿态下的张力向量